Валидация конечной смешанной модели с использованием квазиэкспериментальных и географических данных
Аннотация
В данной работе основное внимание уделяется валидации конечной смешанной модели – одного из самых передовых методов электоральной диагностики. На основе данных, собранных в ходе российских парламентских 2011 г. и президентских выборов 2012 г., в работе была предпринята попытка найти ответы на ряд вопросов. Предсказывает ли новая конечная смешанная модель более или менее корректно результаты, получаемые из альтернативных источников данных, таких как отчёты наблюдателей и автоматизированные системы голосования? Насколько новый метод соответствует нашим теоретическим ожиданиям относительно географического распределения электоральных фальсификаций? Насколько тесно распределение географических кластеров конечных смешанных оценок коррелирует с географическими кластерами оценок, полученных с помощью других методов диагностики? Для ответа на все эти вопросы задействуется широкий спектр доступных методов: метод псевдорандомизации, корреляционный анализ и методы электоральной диагностики. Основные результаты нашего исследования показывают, что конечные смешанные оценки, по-видимому, адекватно отражают электоральные аномалии, что делает их полезными при проведении исследований электоральных фальсификаций.
1. Введение
Электоральная диагностика придаёт особую ценность многочисленным усилиям по обеспечению чистых выборов в мире, снабжая исследователей инструментами и методами, помогающими выявить и оценить масштаб электоральных фальсификаций в официальных данных. Тем самым, электоральная диагностика способствует получению необходимых статистических доказательств наличия или отсутствия оснований для разного рода обвинений, связанных с фальсификациями выборов. Поскольку речь идет о фальсификациях, не поддающихся простому измерению, разнообразные валидационные исследования, проливающие свет на степень достоверности, с которой различные методы способны диагностировать аномалии, становятся неотъемлемой частью исследований в данной области. Любые вспомогательные данные, содержащие информацию об электоральных аномалиях и нарушениях и собранные в рамках какого-либо объективного процесса, могут способствовать проверке валидности получаемых оценок.
Новый прорыв в электоральной диагностике, связанный с появлением позитивной эмпирической модели фальсификации выборов [33], не только открывает новые возможности перед учеными и практиками, занимающимися исследованием фальсификаций выборов в различных избирательных контекстах, но и поднимает вопрос о валидности нового метода измерения. Ситуация в России, очевидно, предоставляет благоприятные возможности для проверки этой новой методологии. Используя как данные по российским парламентским выборам 2011 г. и президентским выборам 2012 г., отмеченным фальсификациями [26; 27; 9; 53], так и вспомогательные квазиэкспериментальные данные, можно оценить валидность нового метода диагностики.
Новый метод – один из множества методов электоральной диагностики. За последние годы их ассортимент значительно расширился, начиная с различных цифровых тестов, таких как первые значащие цифры в совокупных числах голосов [6], вторые значащие цифры [43; 32], последние цифры в числах голосов [4] или последние цифры в процентах [23], и заканчивая различными эмпирическими методами на основе распределения, предложенными Мягковым и др. [40], Шпилькиным [58], регрессионным анализом [56], а также параметрическими моделями электоральной фальсификации [26; 33]. Важно иметь в виду, что любой метод электоральной диагностики несет в себе не только различные имплицитные или эксплицитные допущения относительно механизма генерации «чистых данных», но и по-разному релевантен в зависимости от специфики электорального контекста и целей исследования.
Очевидные успехи в разработке методологии электоральной диагностики позволили Уолтеру Мебейну и Кириллу Калинину при финансовой поддержке Агентства США по международному развитию (USAID) создать веб-сайт «Инструментарий электоральной диагностики» (Election Forensics Toolkit). Основные методы электоральной диагностики, такие как получение конечной смешанной оценки и построение карт, демонстрирующих результаты кластерного анализа, основываются на использовании данного Инструментария (https://www.iie.org/Research-and-Insights/Publications/DFG-UM-Publication). Проект был специально разработан для обеспечения доступности методов электоральной диагностики политикам, практикам и ученым. Помимо электоральных данных это исследование также прибегает к анализу квазиэкспериментальных данных: двух квазиэкспериментов, основанных на данных по наблюдению за выборами, и информации об установке автоматизированных систем голосования.
Данное исследование будет сосредоточено на проверке оценок конечной смешанной модели Уолтера Мебейна по ряду причин. Во-первых, будучи одним из наиболее передовых методов электоральной диагностики, он продолжает находиться на стадии разработки и потому требует серии проверок валидности. Во-вторых, если предположить, что конечная смешанная модель дает верные оценки, в отличие от других методов диагностики, она представляет наибольшую содержательную ценность для исследователей и практиков, позволяя получить оценки вероятности фальсификаций по двум различающимся механизмам. В-третьих, конечная смешанная модель предоставляет расчеты на самом низком уровне агрегирования – как правило, на уровне участков, что делает проверку валидности её оценок более точной, особенно при наличии вспомогательных данных.
В данной работе предпринимаются попытки поиска ответов на ряд вопросов. Насколько корректно новая конечная смешанная модель предсказывает результаты доступных квазиэкспериментов? Насколько полученные оценки соответствуют нашим теоретическим ожиданиям относительно географического распределения электоральных фальсификаций? Насколько точно распределение географических кластеров наших оценок в конечной смешанной модели коррелирует с географическими кластерами, выстроенными на основе общеизвестных методов электоральной диагностики? Чтобы ответить на все эти вопросы, нами используется широкий спектр доступных методов: псевдорандомизация, корреляционный и кластерный анализы.
Структура работы выглядит следующим образом. В разделах 2 и 3 дается подробный обзор литературы по методологии электоральной диагностики. В разделе 4 описывается контекст российских выборов в 2011–2012 гг. и обсуждается доступность соответствующих данных. Раздел 5 содержит методологические инструменты и нуждающиеся в проверке гипотезы. В разделе 6 представлены общие выводы эмпирического анализа квазиэкспериментальных данных на уровне участков и районов с использованием псевдорандомизации, корреляционного и кластерного анализа. В заключительной части делаются выводы и обсуждаются перспективы будущих исследований.
2. Измерение электоральных фальсификаций
Долговечность авторитарных режимов в значительной степени обусловлена их способностью эффективно подрывать электоральные вызовы со стороны оппозиции через средства массовой информации, государственные институты или сами выборы. В этом смысле качество выборов в подобных режимах вызывает озабоченность, поскольку автократы нередко прибегают к электоральным манипуляциям, направленным на минимизацию неопределенности в отношении благоприятных для них результатов выборов, а также деморализацию политической оппозиции посредством демонстрации своей «манипулятивной» силы [29; 13; 47]. Хотя исследования электоральных фальсификаций и усложняются их скрытым характером, оставляемые ими следы в официальных итогах голосования могут оказаться полезными для ученых, занимающихся электоральными исследованиями. С практической точки зрения сложность этой задачи усугубляется проблемой доступности детализированных данных, необходимых для построения сложных объяснительных моделей, а также разнообразием существующих политических и избирательных систем, заметно усложняющих проведение сравнительных исследований в области электоральной диагностики.
Одним из самых популярных методологических подходов в электоральной диагностике служат цифровые тесты, построенные на сравнении эмпирических распределений с заранее заданными теоретическими распределениями. Среди наиболее широко используемых тестов можно упомянуть тест первых цифр совокупных итогов голосования [6], вторых значащих цифр [43; 32], последних значащих цифр в числах голосов [4] или последних цифр в процентах [23]. Например, в контексте честных выборов теоретическое распределение первой и второй цифры, как ожидается, должно следовать закону Бенфорда (2BL), когда как последние цифры в числах голосов или процентах должны следовать равномерному распределению. В отличие от вышеупомянутых тестов, тест для вторых значащих цифр оказался ненадёжным инструментом электоральной диагностики, его использование больше не практикуется.
Следуя подходу Мебейна [34], Бебер и Скакко [3] предлагают тест последней цифры, основанный на идее, что при чистых результатах выборов последние цифры от 0 до 9 должны следовать закону равномерного распределения. Авторы также приводят ряд допущений теста: а) результаты выборов не кластеризуются в узком диапазоне чисел, оставляя место для незначительных различий в размерах избирательных участков или округов, электоральной поддержке или явке; б) результаты голосования не должны содержать много одно- и двузначных чисел, т.е. метод должен исключать кандидатов-аутсайдеров или малые избирательные участки. При соблюдении этих условий любое статистически значимое отклонение от равномерного распределения может быть связано с фальсификацией результатов выборов. Анализ последней цифры может быть распространен на любые другие электоральные переменные, отвечающие вышеперечисленным условиям (далее в тексте {CL}). Метод анализа последней цифры получил свое дальнейшее развитие с появлением теста последней цифры в процентах, обоснованием которого послужила теория сигнальных игр. В частности, согласно этой теории, наличие аномалий в последних значащих цифрах может быть вызвано существованием сигнального механизма, с помощью которого региональные руководители информируют Кремль о своей лояльности через готовность использовать имеющиеся административные ресурсы в интересах центра [23]. В данном случае самым простым и наиболее легко обнаруживаемым способом сообщить основную информацию вышестоящим инстанциям служат округленные проценты электоральной поддержки инкумбента (далее в тексте {P05}).
Нецифровой подход к анализу фальсификаций использует иные методы. К примеру, электоральные аномалии могут определяться как разница между теоретически заданным нормальным или унимодальным распределением явки/голосования и эмпирически наблюдаемым. Анализ перетоков избирателей между выборами в различных гетерогенных условиях – еще один метод электоральной диагностики [40]. В ряде исследований также предлагается метод корреляционного или регрессионного анализа для расчета взаимосвязи между показателями явки и голосования [56; 52]. Непараметрический подход, разработанный Сергеем Шпилькиным, будучи одним из наиболее эффективных методов расчета масштабов фальсификаций, основан на построении гистограмм для явки и электоральной поддержки [58]. Подробный обзор методологии основных методов электоральной диагностики дается в работе Хиккена и Мебейна [18].
Поскольку измерение электоральных фальсификаций сопряжено со значительными сложностями, проведение валидационных исследований в этой области является принципиально важной задачей. К сожалению, отдельно взятый метод электоральной диагностики не только основывается на различных имплицитных или эксплицитных допущениях относительно механизма генерации «чистых данных», но и в зависимости от электорального контекста может по-разному проявляться. К тому же пока не существует какого-либо очевидного консенсуса относительно сравнительной валидности методов электоральной диагностики, поскольку подобных исследований пока не проводилось. Эта задача дополнительно усложняется наличием различных шкал (цифровой, вероятностной или магнитудной), различных уровней (участков, районов или более высоких уровней агрегирования), а также различной чувствительностью каждого метода к скрытым механизмам фальсификаций.
Совсем недавно Калининым и Мебейном [24] было проведено первое валидационное исследование, ставившее своей целью сравнительный анализ оценок, полученных при помощи конечной смешанной модели, и оценок, полученных с применением метода Сергея Шпилькина, где в качестве исходной базы для сравнения использовались субъективные оценки Александра Киреева. Выводы Калинина и Мебейна [24] показывают, что метод конечной смешанной модели и подход Шпилькина хотя примерно и согласуются в отношении ранжирования регионов с высоким или низким уровнем фальсификаций, однако оба метода расходятся по абсолютным величинам оценки фальсификаций. При использовании субъективных оценок Киреева [54] в качестве исходных оказывается, что, хотя оценки конечной смешанной модели не так точны по сравнению с оценками Шпилькина [57] при разграничении «средней фальсификации» и «нулевой фальсификации», они лучше соотносятся с категориями Киреева при разграничении «сильной фальсификации» и «средней фальсификации» [24].
В этой статье особое внимание уделяется квазиэкспериментальной валидации конечной смешанной модели и анализу географического распределения конечных смешанных оценок фальсификаций. До недавнего времени квазиэкспериментальные исследования, касавшиеся мониторинга выборов, помогали преодолеть ограничения и допущения электоральной диагностики. Сделавшись неотъемлемой частью усилий по продвижению чистых и справедливых выборов в мире, мониторинги создали возможности для внешней валидационной проверки выборов [5]. Использование мониторингов авторитарными режимами связано не только с желанием автократов продемонстрировать населению страны и международному сообществу свою приверженность идее выборов, но и намерением деморализовать политическую оппозицию как масштабом своей поддержки, так и манипулятивным характером выборов [46]. С методологической точки зрения присутствие наблюдателей на отдельно взятых участках, способное предотвратить махинации, помогает в расчете масштабов электоральных фальсификаций в стране. Исследования, демонстрирующие уменьшение фальсификаций на участках с присутствующими наблюдателями, служат тому подтверждением [20; 21; 25; 49]. При этом стоит учитывать стратегическую адаптацию поведения администраторов через применение иных, менее очевидных способов манипулирования [48] или смещение электоральных фальсификаций на сопредельные территории, лишенные мониторинга [22].
Аналогичным образом внедрение новых технологий, связанных с голосованием или наблюдением за выборами, как правило, влияет на поведенческие стратегии самих организаторов выборов. Воздействие технологий на электоральное поведение изучалось, в частности, Херроном [17], Бадером [2] и Сьобергом [48]. Так, Херрон [17] утверждает, что в Азербайджане организация пассивного мониторинга посредством установки веб-камер приводит к снижению электоральной поддержки существующего режима. Другой интересный аспект исследования касается установки автоматизированных систем голосования. Так, установка оборудования для голосования с оптическим сканированием или системы голосования с прямой записью (DRE) на избирательных участках способна снизить уровень традиционных электоральных фальсификаций, таких как вброс или переброс избирательных бюллетеней [2]. Отсюда следует, что внедрение новых технологий голосования на ограниченном числе избирательных участков способно не только предотвратить использование новых мошеннических стратегий, но и препятствовать искусственному завышению результатов выборов традиционными способами. Активное участие наблюдателей в поствыборных аудитах с использованием вероятностных выборок позволяет выявить и предотвратить электоральные махинации, тем самым повышая уровень доверия общественности к результатам выборов [10; 41]. Однако, к сожалению, подобного рода исследования редко основываются на случайном отборе наблюдателей на участки, к примеру, дорогостоящих многоуровневых стратифицированных выборках, тем самым, порождая ошибки в исследовательских выводах [19].
3. Позитивные модели электоральной фальсификации
Настоящий прорыв в методологии электоральной диагностики произошел с появлением позитивной эмпирической модели электоральной фальсификации, предложенной Климеком и др. [26]. Модель Климека выстраивается вокруг партии/кандидата, набравшей большинство голосов, в том числе, за счет других партий/кандидатов или не явившихся на выборы избирателей. Модель строится на двух компонентах. Первый компонент включает явку и число голосов, отданных за победителя в условиях чистых выборов. Результаты чистых выборов моделируются из нормального распределения со средним значением и стандартным отклонением, полученными из первого локального максимума эмпирической функции распределения. Второй компонент учитывает интенсивность аномалий, связанных с возможными электоральными фальсификациями и рассчитывается на основе информации, полученной из правой части эмпирической функции распределения. Данная модель помогает получить количественные оценки аномалий внутри избирательного участка по двум отдельно взятым параметрам: инкрементная фальсификация с умеренным перераспределением голосов и предельная фальсификация со значительным перераспределением голосов в пользу кандидата или партии власти. Каждый из параметров отражает различные механизмы фальсификаций. Так, переброс избирательных бюллетеней в основном выражен в инкрементных фальсификациях, тогда как вброс – в предельных.
Согласно Мебейну [33], подход Климека предполагает, что чистые явка и доля голосов победителя описываются двумя нормальными распределениями: \(\tau_i \sim \mathcal{N}(\tau, \sigma_\tau)\) и \(\nu_i \sim \mathcal{N}(\nu, \sigma_{\nu})\). Случаи манипуляций с голосами представлены в виде разных пропорций голосов за оппозицию или не явившихся избирателей, идущих в пользу победившего кандидата. При инкрементной фальсификации мы имеем \(x\) – долю голосов не явившихся избирателей, засчитывающуюся лидирующей партии/кандидату, и \(x^\alpha\) – долю оппозиционных голосов, идущих в пользу победителя. При предельной фальсификации мы имеем \(1-y\) голосов не явившихся, засчитанных лидирующей партии/кандидату, и \((1-y)^\alpha\) – долю подлинных голосов за оппозицию, идущих победителю. Здесь \(\alpha\) фиксирует природу фальсификаций: кражу голосов у оппозиции или приписывание несуществующих голосов в пользу кандидата-лидера. Если \(\alpha=1\), то оба типа электоральной фальсификации одинаково влияют на результаты голосования; если \(\alpha<1\), то кража голосов у оппозиции имеет первостепенное значение; если \(\alpha>1\), преобладает приписывание победителю несуществующих голосов из числа не явившихся избирателей.
Инкрементная фальсификация, \(f_i\), измеряет вероятность того, какая доля голосов не явившихся избирателей превращается в голоса, где \(x_i \sim |\mathcal{N}(0, \theta)|\). Число голосов, отошедших лидирующей партии/кандидату посредством данного типа фальсификации, рассчитывается как \( W_i=N_i(\tau_i \nu_i+ x_i(1-\tau_i) + x_i^\alpha(1-\nu_i) \tau_i \), число голосов за оппозицию \(O_i=N_i(1-x_i^{\alpha}) (1-\nu_i) \tau_i\), и, наконец, число не явившихся на выборы \(A_i=N_i(1-x_i)(1-\tau_i)\).
Предельная фальсификация, \(f_e\), измеряет вероятность того, какая доля не явившихся избирателей не превращается в реальные голоса: \(y_i \sim |\mathcal{N}(0, \sigma_x)|\), \(\sigma_x=0.075\), \(0 < y_i < 1 \). Отсюда \(W_i=N_i(\tau_i \nu_i+ (1-y_i)(1-\tau_i) + (1-y_i)^\alpha(1-\nu_i) \tau_i)\), \(O_i=N_i(1-(1-y_i)^\alpha) (1-\nu_i) \tau_i\) и \(A_i=N_i y_i (1-\tau_i)\).
Наконец, если фальсификация отсутствует (чистое голосование) с вероятностью \(f_0=1-f_i-f_e\), то \(W_i=N_i \tau_i \nu_i\), \(O_i = N_i \tau_i(1-\nu_i)\) и \(A_i=N_i(1-\tau_i)\).
Несмотря на гибкость модели на разных уровнях агрегирования, рассчитанные показатели аномалий подвержены проблеме неоднородности данных. Например, утверждения авторов о наличии предельных фальсификаций в значительной части округов со 100% явкой и всеми голосами, отданными за одну партию, вполне можно объяснить спецификой некоторых участков, находящихся в небольших сельских поселениях, воинских частях или тюрьмах.
Мебейн [33], основываясь на работах Климека и др. [26], далее развивает эту модель. Подобно Климеку, модель Мебейна помогает предсказать происхождение многогорбного распределения в явке и голосовании. Модель рассматривает случаи чистого голосования, инкрементных фальсификаций и предельных фальсификаций в качестве трех отдельных компонентов конечной смешанной модели. Модель включает в себя три переменные: общее число зарегистрированных избирателей, общее число проголосовавших избирателей и число избирателей, проголосовавших за победившего кандидата. Подбор параметров модели осуществляется с помощью функции правдоподобия с имитируемыми ненаблюдаемыми переменными, взятыми из Климека и др. [26]. Основные параметры \(\tau_i\), \(\nu_i\), \(x_i\) и \(y_i\) генерируются из нормальных распределений. Оценка максимального правдоподобия позволяет получить оценки параметров, максимизирующие вероятность того, что наблюдаемые данные произведены процессом, описанным моделью Мебейна.
Согласно Мебейну [33], модель принимает следующий вид:
\(F({W, O, A~|~N; \Psi}) =\sum\limits_{j \in\{0,i,e\}} f_j \prod\limits_{i=1}^{n} g_{j W} (W_i~|~N_i; \Psi) g_{jA}(A_i~|~N_i; \Psi)\)
В модели \(f_0\), \(f_i\) и \(f_e\) – вероятности нулевой фальсификации или чистого голосования, инкрементной фальсификации и предельной фальсификации, где \(f_0+f_i+f_e=1\); \(g_{j W} (W_i~|~N_i; \Psi)\) и \(g_{jA}(A_i~|~N_i; \Psi)\) – условные плотности со скалярными параметрами, взятыми из модели Климека, содержащиеся в векторе \(\Psi=(\alpha, \nu, \tau, \sigma_{\nu}, \sigma_{\tau}, \theta)'\). Как обычно, в конечной смешанной модели [31], вероятности \(f_0\), \(f_i\) и \(f_e\) являются средними значений правдоподобия наблюдений, и таковыми выступают функции всех оценок для параметров в \(\Psi\). Модель описывает совместную плотность наблюдаемого числа голосов, отданных за победившую партию \(W_i\), наблюдаемое число голосов, отданных за другие партии \(O_i\), и наблюдаемое число не голосовавших \(A_i\), т.е. \((W_i;O_i;A_i)\), которые в совокупности обусловлены числом избирателей, имеющих право голоса на каждом избирательном участке \(N_i\). Параметры модели оцениваются при помощи алгоритма максимизации ожиданий (EM) в пакете rgenoud для языка программирования R [39].
Параметры модели рассчитываются как на самом высоком, так и на самом низком уровне агрегирования данных. На самом высоком уровне оцениваются следующие параметры: \(f_i, f_e\) – условные вероятности инкрементной и предельной фальсификаций; \(\alpha\) – параметр, указывающий на украденные или приписанные голоса; \(\tau\), \(\sigma_\tau\) и \(\nu\), \(\sigma_\nu\) – соответственно среднее значение и стандартное отклонение доли явки, а также среднее и стандартное отклонение доли голосов за лидирующую партию/кандидата при отсутствии фальсификаций; \(\theta\) – параметр, указывающий, увеличивает ли инкрементная фальсификация число голосов за лидирующую партию или нет. На самом низком уровне агрегирования (как правило, на уровне участков) особый интерес представляет расчёт нескольких величин: \(f_{ii}, f_{ei}, f_{0i}\) – вероятности фальсификации на уровне избирательных участков и \(p_{ii}, p_{ei}, p_{0i}\) – масштабы электоральных фальсификаций на уровне избирательных участков [33]. Хотя алгоритм EM позволяет получить оценки условной вероятности того, что каждое наблюдение относится к разным механизмам фальсификации, но не даёт оценок неопределенности вероятностей на уровне участков. Модель успешно воспроизводит механизмы фальсификаций в мажоритарных избирательных системах с явным победителем (президентские выборы или одномандатные округа), однако её применение в отношении пропорциональных избирательных систем без явного победителя может оказаться проблематичным. Более того, подобно модели Климека, конечная смешанная модель также полагается на многогорбность в распределении явки и голосования, хотя природа наблюдаемой мультимодальности может быть связана с нормальными политическими процессами, к примеру, стратегическим голосованием. Поскольку зависимость от допущения о мультимодальности может потенциально привести к ложно-положительным результатам, использование контекстной и вспомогательной информации в каждой конкретной ситуации имеет решающее значение для определения происхождения электоральных аномалий. Аналитическая интеграция оценок конечной смешанной модели с оценками, полученными из альтернативных источников данных, такими как отчёты наблюдателей или жалобы после выборов -- наиболее эффективная стратегия в рамках электоральной диагностики.
4. Контекст и данные
Россия имеет длительную историю нечестных выборов, на которых подавление эффективной политической конкуренции сочетается с искусственно завышенной электоральной поддержкой кремлевских партий или кандидатов. В 2000-е гг. растущие авторитарные тенденции в российской политической системе еще более усугубили проблему масштабных фальсификаций и электоральных манипуляций, сделавших российские выборы важным предметом научных исследований. Низкое качество российских выборов в разных избирательных циклах и на разных уровнях организации выборов анализируется во многих научных работах [52; 36; 40; 35; 58].
Избирательный цикл 2011–2012 гг. ознаменовался переходом президентской власти от Дмитрия Медведева вновь к Владимиру Путину. Осенью 2011 г. тогдашний президент Медведев предложил тогдашнему премьер-министру Путину баллотироваться на третий срок. Эта заранее спланированная рокировка вызвала широкое общественное недовольство и задала тон как предстоящим российским парламентским, так и президентским выборам. Парламентские выборы привели к сокрушительному поражению партии власти «Единая Россия», утратившей свое конституционное большинство в две трети, даже несмотря на манипулятивный характер выборов и многочисленные обвинения в фальсификациях. В свою очередь несправедливые и нечистые выборы спровоцировали рост массовых протестов в Москве и Санкт-Петербурге, вынудив Кремль принять экстренные меры, направленные на обеспечение избирательной прозрачности предстоящих мартовских президентских выборов. Были установлены прозрачные урны для голосования (одна треть избирательных участков использовала прозрачные урны), и каждый избирательный участок в стране был оснащен веб-камерой. Наряду с протестами выборы, особенно президентские, были отмечены значительным увеличением гражданской активности и повышенным вниманием к наблюдению за выборами, организованному в рамках проектов «Голос», «Гражданин Наблюдатель» и «Лига избирателей». Превентивные действия российских избирательных комиссий по оснащению избирательных участков веб-камерами и прозрачными урнами для голосования, а также гражданское участие в наблюдении за выборами помогли получить дополнительные данные для нашего валидационного исследования.
Разнообразные источники, основанные на электоральных, опросных данных, а также отчетах наблюдателей, говорят о распространенности фальсификаций на российских выборах 2011–2012 гг., существенно повлиявших на их итоги [27; 53; 9]. Согласно некоторым оценкам, в 2012 г. фальсификации электоральной поддержки Путина и явки могли составлять 5% и 10% соответственно [53]; по другим оценкам, процент избирательных участков с фальсификациями достигал около 40% в 2012 г. и 60% в 2011 г. [26].
Наличие альтернативных источников данных, таких как отчёты наблюдателей и информация об установке автоматизированных систем голосования, позволяет провести методологическую валидацию метода Мебейна. Во-первых, предполагается, что простое физическое присутствие наблюдателей, скорее всего, изменит поведенческие стратегии организаторов, помешав им совершить фальсификации. Во-вторых, установка автоматических систем голосования на отдельных избирательных участках делает традиционные манипуляции, такие как вброс или переброс бюллетеней, чрезвычайно затратными для организаторов, тем самым уменьшая их число. Установка веб-камер также способна повлиять на стратегии организаторов фальсификаций, ограничивая возможности для традиционных способов манипулирования. Оба подхода особенно полезны при предположении, что наблюдатели, автоматические системы голосования и видеокамеры приписаны к участкам случайным образом, тем самым, позволяя рандомизации сбалансировать экспериментальные и контрольные группы по различным признакам. Подобный способ оценки масштабов электоральных фальсификаций и проверки валидности конечной смешанной модели без привязки к каким-либо допущениям полезен при расчете фальсификаций.
Поскольку в нашем исследовании мы имеем дело с квазиэкспериментальными (по сути, обсервационными), а не с экспериментальными данными в чистом виде, необходимо учитывать различия в наблюдаемых ковариационных распределениях между нашими контрольной и экспериментальной группами. Помимо этого, нужно сделать допущение о том, что присутствие наблюдателей или наличие автоматизированных систем голосования на участках не изменяют электоральное поведение избирателей. К примеру, избиратели могут счесть, что их волеизъявление отслеживается с помощью определенных функций системы КОИБ/КЭГ, связанных с созданием файла, содержащего изображение бюллетеня с отметкой времени голосования [16]. Несмотря на то, что размещение веб-камер, казалось бы, даёт много информации о чистоте выборов, их установка почти на всех избирательных участках в 2012 г. сделала невозможным определение контрольной группы, затруднив тем самым расчет масштабов фальсификаций экспериментальным образом. Поэтому для 2012 г. мы ограничимся использованием квазиэкспериментальных данных, основанных на различиях в автоматических системах голосования по участкам. Для анализа выборов 2011 г. мы будем использовать данные наблюдений за выборами в Москве, ранее использовавшиеся в работе Ениколопова и др. [9] и предоставленные Василием Коровкиным. Эти данные были изначально собраны независимой неправительственной организацией «Гражданин Наблюдатель», обучившей более 500 наблюдателей-добровольцев в Москве. Наблюдатели были направлены на 156 избирательных участков, случайно отобранных при помощи систематического отбора (Левада-центр). В своем исследовании Ениколопов и др. [9] пришли к выводу, что простое присутствие наблюдателей на участках сократило долю «Единой России» на 9,3–10,8 п.п. и увеличило число голосов за другие партии. В своем анализе 2012 г. мы используем данные, взятые с веб-сайта проекта СМС-ЦИК, позволяющего наблюдателям оперативно сообщать информацию из протоколов УИКов. Эти данные были загружены с веб-сайта, парсированы и объединены с официальными данными на уровне избирательных участков 2012 г. Процедура довольно проста: телефонные сообщения, содержащие цифры из участковых протоколов, передаются наблюдателями на номер телефона, затем обрабатываются серверами и мгновенно становятся общедоступными через веб-сайт www.sms-cik.org. К сожалению, данная процедура подразумевает, что наблюдатели самоотбираются, а не случайным образом распределяются по участкам согласно экспериментальному плану.
Географические данные и результаты голосования на обоих выборах были любезно предоставлены Сергеем Шпилькиным. На выборах 2011 и 2012 гг. использовались два типа новых устройств для голосования. Первый, КОИБ (комплекс обработки избирательных бюллетеней), представляет собой автоматическую систему голосования с оптическим сканированием бюллетеней и избирательной урной из полупрозрачных материалов. Одна из его функций – создание файла с отсканированным бюллетенем, на котором указано время голосования, и передача результатов выборов по телекоммуникационной сети в избирательную комиссию более высокого уровня. Второй, КЭГ (комплекс электронного голосования), включает в себя электронные машины для голосования с прямой записью (DRE) на основе сенсорного дисплея, на который выводится список кандидатов и партий для непосредственного выбора. Результаты голосования хранятся в памяти КЭГ, а также печатаются на недоступной избирателю бумажной ленте (см. рис. A1 (a), (b) в Приложении A).
Основываясь на подходе Мягкова и др. [40], Бадер [2] применил метод «разность в разности», показав, что для избирательных участков, оборудованных КОИБ, в 2011 г., но не в 2012 г. характерны снижение уровня явки (-3,8%) и доли голосов за правящую партию (-4,8%). Для участков, оборудованных КОИБ, в 2012 г., но не в 2011 г. влияние КОИБ незначительно и выражено в снижении явки всего на 0,4% и поддержки основного кандидата – на 0,6%. Поскольку критерии отбора участков для размещения КОИБ/КЭГ более или менее очевидны (например, КЭГ преимущественно используются в этнических регионах в качестве двуязычного устройства) для устранения систематических различий между сравниваемыми группами можно прибегнуть к псевдорандомизации [17; 48]. К сожалению, предлагаемая процедура не решает множество проблем, связанных с неслучайным отбором и отсутствием предварительных данных.
Таким образом, наше валидационное исследование построено на анализе следующих данных:
• Официальные данные на уровне участков, используемые в рамках электоральной диагностики, включающей конечную смешанную модель.
• Данные наблюдателей в Москве (парламентские выборы, 2011 г.) и по стране в целом (президентские выборы, 2012 г.).
• Данные о географическом распределении КОИБ/КЭГ/наблюдателей на выборах 2011 г. и 2012 г.
5. Аналитическая стратегия
Наш анализ основан на квазиэкспериментальных данных с использованием псевдорандомизации, корреляционного и кластерного анализа. Предложенная аналитическая стратегия включает в себя: 1) проверку валидности оценок конечной смешанной модели с помощью квазиэкспериментальных данных полученных по итогам наблюдения за выборами, а также данных о географическом распределении КОИБ/КЭГ; 2) проверку валидности оценок конечной смешанной модели с использованием информации о географическом распределении электоральных фальсификаций, описанных в теоретических источниках.
5.1. Проверка валидности с использованием квазиэкспериментальных данных
Для решения проблемы, связанной с устранением систематических различий между сравниваемыми группами, прибегнем к псевдорандомизации. В результате процедуры, выполненной с помощью пакета Matching для языка программирования R [45], наши квазиэкспериментальные группы сбалансированы по ключевым ковариантам: тип региона (республика/область), тип поселения (город/сельский район) и размер участка. Первоначально приоритетной процедурой был автоматизированный поиск пар избирательных участков с наблюдателями/автоматической системой голосования и участками без наблюдателей/с обычными урнами для бумажных бюллетеней на основе алгоритма k-ближайших соседей, однако значительные стандартные ошибки не позволили воспользоваться данным подходом. Включенные в модель псевдорандомизации переменные связаны со спецификой голосования в отдельных местах. Арбатская [51], анализируя российские выборы 1996-2000 гг., говорит о различиях политического участия в регионах, которые частично определяются административным вмешательством в избирательный процесс, а также иными факторами, такими как тип региона, городское/сельское поселение, тип промышленной структуры, сезонные эффекты и т.д. В республиках обычно проявляется больше электоральной поддержки действующей власти по сравнению с областями. Более того, эмпирические данные свидетельствуют о том, что российские национальные республики по сравнению с областями обладают более совершенной «машинной политикой», позволяющей обеспечить беспрецедентный уровень мобилизации избирателей [36; 23]. В данном случае под «машинной политикой» подразумевается создание организаций, т.н. «политических машин», обеспечивающих электоральную поддержку путем предоставления гражданам материальных выгод в обмен на их голоса [12]. Как правило, эти организации расположены в национальных республиках и автономных округах с плотными этническими социальными сетями и сельскими районами, с населением, зависимым от местных начальников [30; 15; 12].
Следовательно, включив в модель псевдорандомизации (propensity score model) три переменные, характеризующие избирательный участок (тип региона, городское/сельское поселение, размер участка), мы можем учесть существование гетерогенности избирательных практик на различных уровнях агрегирования данных.
5.2. Проверка валидности с использованием географического распределения электоральной фальсификации
В России ожидаемое географическое распределение электоральных фальсификаций тесно связано с силой политических машин в регионах. Хейл [15] утверждает, что в 2000-е гг. проявилась способность региональных губернаторов и глав республик превращать сети политического патронажа в политические машины, «заточенные» под обеспечение необходимого уровня электоральной поддержки существующей власти. Использование административного ресурса подразумевает, что «региональные власти оказывают различные виды давления на избирателей для обеспечения желаемых результатов выборов» [11]. В постсоветские годы республики с большой охотой шли на сделки с центром и в большей степени были склонны к манипуляциям с выборами в подвластных им регионах [50; 44]. Главы республик более эффективно контролировали голосование, наказывая или вознаграждая избирателей, чем это делали их коллеги из других регионов [14: 231]. Отсюда можно ожидать, что национальные республики и регионы с сильными политическими машинами вероятнее всего станут местом крупнейших кластеров фальсификаций.
В каких регионах, скорее всего, будут наблюдаться подобные кластеры? Список таких регионов может быть составлен с учетом экспертных оценок демократичности, рассчитанных Николаем Петровым и Алексеем Титковым [55]. К этим регионам в нисходящем порядке демократичности могут быть отнесены Республика Дагестан, Омская область, Орловская область, Тамбовская область, Республика Карачаево-Черкесия, Ямало-Ненецкий автономный округ, Костромская область, Пензенская область, Республика Татарстан, Республика Саха (Якутия), Брянская область, Ростовская область, Смоленская область, Республика Хакасия, Республика Адыгея, Белгородская область, Республика Марий Эл, Республика Башкортостан, Кемеровская область, Курганская область, Республика Тыва, Республика Калмыкия, Республика Северная Осетия, Курская область, Республика Кабардино-Балкария, Республика Ингушетия, Республика Мордовия, Чукотский автономный округ и Чеченская Республика. Следовательно, если наши оценки в конечной смешанной модели чувствительны к проявлению слабого демократического климата и присутствию сильных региональных политических машин, то большинство кластеров электоральных фальсификаций будет находиться в этих регионах.
Нахождение кластеров электоральных фальсификаций в сельских районах с более высокой концентрацией социальных связей и более низким уровнем анонимности по сравнению с городской средой также приведет к использованию местных политических машин. Райзингер и Мораски [44] утверждают, что местные политики, играющие важную роль в предоставлении товаров и услуг, будут наиболее успешными в мобилизации поддержки избирателей в соответствующих населенных пунктах. В литературе также отмечается, что наличие тесных социальных связей в сельских районах способствует эффективной мобилизации избирателей, к примеру, в Кыргызстане [7] и в Африке [28]. Отсюда можно предположить, что кластеры электоральных фальсификаций для российских выборов будут размещаться преимущественно в сельской местности.
В этой части исследования используется метод кластерного анализа, который идентифицирует географические паттерны кластеризации как для различных методов электоральной диагностики, так и для различных уровней агрегирования электоральных данных. Данный метод способствует выявлению локальных сгустков схожих фальсификаций.
Мы используем две процедуры оценки, доступные в «Инструментарии электоральной диагностики»: a) анализ горячих точек Getis-Ord \(G_i\) [42], замеряющий разницу между средним значением географически близких к наблюдению \(i\) точек и глобальным средним значением, и b) локальный индекс Морана \(I_i\) , показывающий разницу между значением наблюдения \(i\) и средним значением географически близких к \(i\) точек [1]. Обе статистики используются в отношении отдельно взятых показателей электоральной диагностики: в частности, анализ приводится в разрезе участков в 2012 г. (Getis-Ord \(G_i\)) и районов в 2011 и 2012 гг. (локальный индекс Морана \(I_i\)). Таким образом, можно определить уровни координации приписок и кражи голосов. Кроме того, для получения лучшего представления о том, как методы электоральной диагностики соотносятся друг с другом на уровне участков и районов, на каждом уровне анализа мы используем корреляционный анализ между соответствующими кластерами.
Исходя из вышеизложенного, можно выдвинуть следующие исследовательские гипотезы:
Гипотеза 1. Ожидается, что оценки конечной смешанной модели будут подвержены влиянию со стороны КОИБ/КЭГ и квалифицированных наблюдателей, поскольку на избирательных участках, оборудованных обычными урнами для голосования и без квалифицированных наблюдателей, уровень фальсификаций должен быть выше.
Гипотеза 2. Географические кластеры фальсификаций, полученные на основе оценок конечной смешанной модели, будут размещаться в регионах и районах, демонстрирующих относительно слабый уровень демократичности и присутствие сильных региональных политических машин, каковыми являются национальные республики и сельские районы.
Гипотеза 3. Ожидается наличие сильных корреляций как на уровне избирательных участков, так и районов между географическими кластерами, выстроенными на оценках конечной смешанной модели, и географическими кластерами, рассчитанными с использованием альтернативных методов электоральной диагностики, таких как сигнальные стратегии (тест {P05} для явки и голосования за действующую власть) и последние цифры числа проголосовавших (тест {CL}).
Для проверки приведенных гипотез обратимся к анализу эмпирических данных.
6. Результаты анализа
Согласно результатам расчета конечной смешанной модели на президентских выборах 2012 г. примерно на 8% участках осуществлялась инкрементная фальсификация, примерно на 0,2% – предельная фальсификация; на парламентских выборах 2011 г. эти цифры составляли соответственно 11% и 0,2%. Эти результаты совпадают с нашими первоначальными предположениями о большей распространенности электоральных фальсификаций на парламентских, чем на президентских выборах. Конечная смешанная модель дает наиболее консервативные оценки вероятностей фальсификаций по сравнению с оценками Климека, показываюшими наличие фальсификаций на 64% участков для думских и 39% участков для президентских выборов.
Оценки Мебейна [33: табл. 4] иллюстрируют гораздо меньшие масштабы электоральных фальсификаций, составляющие 1,5% на парламентских и 0,68% на президентских выборах. В частности, числа голосов, относящиеся к инкрементной и предельной фальсификации, для выборов 2011 г. составляют 680082 (\(M_i\)) и 260254 (\(M_e\)), а для на президентских выборов 2012 г. – 292339 (\(M_i\)) и 189912 (\(M_e\)) [33: 13; 24]. Полученные расчеты не соотносятся с предыдущими исследованиями, оценивающими масштаб электоральных фальсификаций в диапазоне от 5% до 10% [53]. Аналогично вероятностям, полученные из конечной смешанной модели оценки фальсификации Мебейна [33], являются наиболее консервативными.
Обратимся к более подробному анализу данных. В таблице 1 показано влияние автоматизированных систем голосования и наблюдателей на явку и голосование в 2012 г. Как упоминалось ранее, для уменьшения потенциальных искажений из-за отсутствия случайного отбора в экспериментальную группу мы прибегли к модели псевдорандомизации, выстроенной на основе таких ковариат как: число зарегистрированных избирателей, место жительства (город/село) и регион (республика/область). Неудивительно, что влияние КОИБ на результаты голосования за Путина отрицательное: доля голосов в его поддержку на участках с КОИБ ниже на 3,6 п.п. по сравнению с участками без КОИБ, тогда как за других кандидатов изменения остаются положительными или статистически незначимыми. Иными словами, по сравнению с КОИБ участки оборудованные традиционными урнами дают Путину статистически значимую завышенную поддержку, возможно, связанную с фальсификацией выборов. Оба показателя в конечной смешанной модели, \(f_i\) и \(f_e\), соответствуют нашим теоретическим ожиданиям, указывая на статистически значимое отрицательное влияние КОИБ на фальсификации: -0,6 и -0,02 п.п. соответственно. КЭГ демонстрируют более неоднозначные результаты: эта технология приводит к завышению доли голосов за Путина на 3,5 п.п. и предельных фальсификаций на 4,2 п.п. Похоже, присутствие наблюдателей снижает поддержку Путина на 9 п.п. и явку примерно на 2 п.п. с предельно значимым коэффициентом \(f_i\). Наконец, выявленные наблюдателями нарушения, по-видимому, не влияют на показатели явки или доли голосов. Одно из объяснений тому, что КЭГ демонстрируют более высокий уровень фальсификаций по сравнению с традиционными урнами для голосования — их малый размер и мобильность, позволяющие использовать это оборудование в небольших населенных пунктах или в сельских районах с более развитыми социальными связями и низким уровнем анонимности. Вдобавок использование КЭГ в отдаленных районах сопряжено с отсутствием надлежащего наблюдения за выборами и повышенной вероятностью нарушений выборных процедур.
Таблица 1: Влияние КОИБ/КЭГ и наблюдателей на долю явки и итоги голосования, 2012 год
| КОИБ | КЭГ | Наблюдатели | Нарушения | |
| Путин | -0.03*** | 0.035* | -0.087*** | 0.011 |
| (0.002) | (0.012) | (0.003) | (0.014) | |
| Жириновский | -0.001 | -0.007* | -0.005*** | -0.006 |
| (0.001) | (0.003) | (0.001) | (0.004) | |
| Зюганов | 0.008*** | -0.027*** | 0.004* | -0.011 |
| (0.001) | (0.006) | (0.002) | (0.008) | |
| Прохоров | 0.02*** | 0.009* | 0.074*** | -0.003 |
| (0.001) | (0.004) | (0.002) | (0.014) | |
| Явка | -0.003 | 0.054*** | -0.019*** | -0.012 |
| (0.002) | (0.011) | (0.003) | (0.014) | |
| fi | -0.006* | -0.053* | -0.007x | -0.024 |
| (0.003) | (0.022) | (0.004) | (0.025) | |
| fe | -0.002* | 0.042*** | -0.001 | 0.000 |
| (0.001) | (0.011) | (0.001) | (0.000) | |
| Наблюдения | 5241 | 311 | 1819 | 54 |
Примечание: Псевдорандомизация основана на наборе наблюдаемых ковариат: число зарегистрированных избирателей, проживание (город/село), регион (республика/область).
Данные: данные по выборам на уровне участков объединены с данными КОИБ/КЭГ и наблюдателей (число подобранных пар при псевдорандомизации представлено в строке Наблюдения).
Переменные: Перечисленные переменные показывают разницу в долях голосов за каждого кандидата, явки и оценок конечной смешанной модели между участками с КОИБ и участками с обычными урнами (колонка «КОИБ»), участками с КЭГ и участками с обычными урнами (колонка «КЭГ»), участками с наблюдателями и без наблюдателей (колонка «Наблюдатели»), участками с нарушениями и участками без нарушений (колонка «Нарушения»). Переменные «Путин», «Жириновский», «Зюганов» и «Прохоров» показывают разницу в долях голосов за Владимира Путина, Владимира Жириновского, Геннадия Зюганова и Михаила Прохорова соответственно.
Уровни значимости: \(^{\times}\)p≤ 0.1, *p ≤ 0.05,**p ≤ 0.01, ***p ≤ 0.001.
Аналогичные выводы напрашиваются из анализа таблицы 2: наличие КОИБ увеличивает доли голосов почти всех партий, кроме «Единой России» (-6.7 п.п.), и вместе с этим уменьшает явку (-2 п.п.). Статистика инкрементной фальсификации \(f_i\) демонстрирует снижение на 4 п.п. Напротив, КЭГ вновь положительно влияют на явку и долю голосов за «Единую Россию», повышая их на 6 и 7,4 п.п. соответственно, причем величина инкрементной фальсификации \(f_i\) достигает 5,5 п.п. Это наблюдение подтверждает наши ожидания о наличии заметной разницы в механизмах электоральных фальсификаций между КЭГ и КОИБ.
Таблица 2: Влияние КОИБ/КЭГ на уровень явки и итоги голосования, 2011 г.
| КОИБ | КЭГ | |
| «Справедливая Россия» | 0.022*** | -0.018** |
| (0.001) | (0.006) | |
| ЛДПР | 0.009*** | -0.006 |
| (0.001) | (0.006) | |
| «Патриоты России» | 0.002*** | 0.001 |
| (0.000) | (0.001) | |
| КПРФ | 0.019*** | -0.032*** |
| (0.002) | (0.008) | |
| «Яблоко» | 0.012*** | 0.004* |
| (0.001) | (0.002) | |
| «Правое дело» | 0.001*** | 0.001*** |
| (0.000) | (0.000) | |
| «Единая Россия» | -0.067*** | 0.061** |
| (0.003) | (0.02) | |
| Явка | -0.019*** | 0.074*** |
| (0.003) | (0.014) | |
| fi | -0.039*** | 0.055* |
| (0.004) | (0.027) | |
| fe | -0.001 | 0.006 |
Таблица показана не полностью Открыть полностью
Примечание: Псевдорандомизация основана на наборе наблюдаемых ковариат: число зарегистрированных избирателей, проживание (город/село), регион (республика/область).
Данные: данные об итогах выборов на уровне участков объединены с данными КОИБ/КЭГ и наблюдателей (число подобранных пар при псевдорандомизации представлено в строке Наблюдения).
Переменные: Перечисленные переменные показывают разницу в долях голосов за каждую партию, явки и оценок конечной смешанной модели между участками с КОИБ и участками с обычными урнами (колонка «КОИБ»), участками с КЭГ и участками с обычными урнами (колонка «КЭГ»). Переменные «Единая Россия», «Справедливая Россия», «ЛДПР», «Патриоты России», «КПРФ», «Яблоко» и «Правое дело» показывают разницу в долях голосов, полученных разными партиями.
Уровни значимости: \(^{\times}\)p≤ 0.1, *p ≤ 0.05,**p ≤ 0.01, ***p ≤ 0.001.
Анализ президентских выборов 2012 г. для Москвы показывает, что хотя КОИБ и не оказывают сколько-нибудь значимого влияния на поддержку Путина, они сокращают явку на 6 п.п. и инкрементную фальсификацию на 12 п.п. (см. таблицу 3). Хотя присутствие наблюдателей, по-видимому, способствует снижению поддержки Путина и росту поддержки Прохорова на 2 п.п., ни один из иных показателей электоральной диагностики не демонстрирует статистической значимости. Наконец, выявленные нарушения не оказывают какого-либо статистически значимого воздействия на уровень фальсификаций.
Обращаясь к анализу парламентских выборов в Москве, можно обнаружить больше свидетельств вопиющей фальсификации (см. таблицу 4). Похоже, что КОИБ снизили поддержку «Единой России» на 19 п.п. и данные по явке почти на 12 п.п. при заметном увеличении электоральной поддержки других партий. Показатель инкрементной фальсификации также уменьшился на 11 п.п. Наличие наблюдателей демонстрирует аналогичную картину снижения поддержки «Единой России» почти на 11 п.п. и явки на 6,4 п.п. Важно, что присутствие наблюдателей сокращает инкрементную фальсификацию почти на 5 п.п. Наконец, выявленные нарушения также повлияли на показатели явки и инкрементной фальсификации, сократив оба показателя почти на 3 п.п.
Таким образом, Гипотеза 1 частично подтверждается нашим анализом: на избирательных участках, оборудованных обычными урнами и без квалифицированных наблюдателей фальсификаций ощутимо больше, чем на участках с КОИБ и квалифицированными наблюдателями. Показатель инкрементной фальсификации почти всегда согласуется с этим наблюдением, демонстрируя статистическую значимость с ожидаемым знаком и величиной эффекта. Еще один вывод, который можно сделать – между КЭГ и КОИБ механизмы фальсификаций различны: КЭГ, использующиеся в отдаленных районах, в большей мере подвержены фальсификациям по сравнению с использованием КОИБ, их сдерживающими.
Таблица 3: Влияние КОИБ и наблюдателей на уровень явки и итоги голосования, Москва, 2012 г.
| КОИБ | Наблюдатели | Нарушения | |
| Путин | -0.008 | -0.021*** | -0.028 |
| (0.007) | (0.002) | (0.02) | |
| Жириновский | 0.003 | -0.003*** | 0.002 |
| (0.002) | (0.001) | (0.005) | |
| Зюганов | 0.005x | 0.003*** | -0.001 |
| (0.003) | (0.001) | (0.007) | |
| Миронов | -0.001 | 0.002*** | 0.005x |
| (0.001) | (0.000) | (0.003) | |
| Прохоров | 0.013** | 0.02*** | 0.02 |
| (0.005) | (0.002) | (0.017) | |
| Явка | -0.055*** | 0.004 | -0.022 |
| (0.01) | (0.003) | (0.023) | |
| fi | -0.12*** | -0.003 | -0.053 |
| (0.018) | (0.004) | (0.051) | |
| fe | -0.004 | 0.000 | 0.000 |
| (0.003) | (0.000) | (0.000) | |
| Наблюдения | 253 | 942 | 17 |
Примечания: КОИБ (подобраны пары), наблюдатели (подобраны пары), нарушения (подобраны пары). Псевдорандомизация основана на наборе наблюдаемых ковариат: число зарегистрированных избирателей, данные о проголосовавших в течение дня избирателях.
Данные: данные об итогах выборов на уровне участка объединены с данными КОИБ/КЭГ и наблюдателей (число подобранных пар при псевдорандомизации представлено в строке Наблюдения).
Переменные: Перечисленные переменные показывают разницу в долях голосов за каждого кандидата, явки и оценок конечной смешанной модели между участками с КОИБ и участками с обычными урнами (колонка «КОИБ»), участками с КЭГ и участками с обычными урнами (колонка «КЭГ»), участками с наблюдателями и без наблюдателей (колонка «Наблюдатели»), участками с нарушениями и участками без нарушений (колонка «Нарушения»). Переменные «Путин», «Жириновский», «Зюганов» и «Прохоров» показывают разницу в долях голосов за Владимира Путина, Владимира Жириновского, Геннадия Зюганова и Михаила Прохорова соответственно.
Уровни значимости: \(^{\times}\)p≤ 0.1, *p ≤ 0.05,**p ≤ 0.01, ***p ≤ 0.001.
Таблица 4: Влияние КОИБ и наблюдателей на уровень явки и итоги голосования, Москва, 2011 г.
| КОИБ | Наблюдатели | Нарушения | |
| «Справедливая Россия» | 0.047*** | 0.022*** | 0.002 |
| (0.003) | (0.004) | (0.005) | |
| ЛДПР | 0.051*** | 0.017*** | 0.003 |
| (0.003) | (0.003) | (0.006) | |
| «Патриоты России | 0.005*** | 0.002*** | -0.001 |
| (0.001) | (0.000) | (0.001) | |
| КПРФ | 0.061*** | 0.028*** | -0.001 |
| (0.005) | (0.004) | (0.008) | |
| «Яблоко» | 0.035*** | 0.035*** | 0.009 |
| (0.004) | (0.004) | (0.007) | |
| «Правое дело» | 0.003*** | 0.001*** | 0.000 |
| (0.000) | (0.000) | (0.001) | |
| «Единая Россия» | -0.193*** | -0.108*** | -0.019 |
| (0.012) | (0.011) | (0.016) | |
| Явка | -0.118*** | -0.064*** | -0.027x |
| (0.01) | (0.008) | (0.016) | |
| fi | 0.111*** | -0.045*** | -0.034** |
| (0.015) | (0.008) | (0.012) | |
| fe | 0.000 | 0.000 | 0.000 |
Таблица показана не полностью Открыть полностью
Примечания: КОИБ (подобраны пары), наблюдатели (обычные данные), нарушения (обычные данные). Совпадение основано на наборе наблюдаемых показателей: число зарегистрированных избирателей, данные о проголосовавших в течение дня избирателях.
Данные: данные об итогах выборов на уровне участков объединены с данными КОИБ/КЭГ и наблюдателей (число подобранных пар при псевдорандомизации представлено в строке Наблюдения).
Переменные: Перечисленные переменные показывают разницу в долях голосов за каждую партию, явки и оценок конечной смешанной модели между участками с КОИБ и участками с обычными урнами (колонка «КОИБ»), участками с КЭГ и участками с обычными урнами (колонка «КЭГ»). Переменные «Единая Россия», «Справедливая Россия», «ЛДПР», «Патриоты», «КПРФ», «Яблоко» и «Правое дело» показывают разницу в долях голосов, полученных разными партиями.
Уровни значимости: \(^{\times}\)p≤ 0.1, *p ≤ 0.05,**p ≤ 0.01, ***p ≤ 0.001.
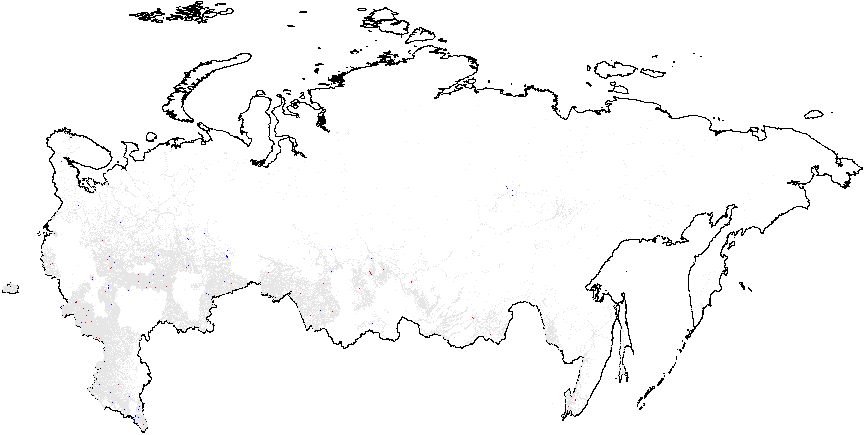
Теперь рассмотрим результаты анализа «горячих точек» выборов в России 2012 г. на основе статистики, рассчитанной с использованием нескольких методов электоральной диагностики. На картах отображены «горячие точки» аномалий, указывающие на разницу между средним значением географически близких к наблюдению \(i\) точек и глобальным средним значением. Красные точки на рисунке 1 (а) указывают на существование кластеров атипично высоких значений, т.е. мест, где локальное среднее интересующей нас переменной значительно превышает глобальное среднее значение \(\bar{f}_i=0.08\). Многие красные точки, свидетельствующие о скоплении участков с высокими вероятностями инкрементной фальсификации, в основном географически сгруппированы в различных этнических регионах, таких как Татарстан, Башкортостан, Мордовия, Чувашия, Дагестан, Чечня, а также некоторых российских областях (Белгородской, Воронежской и других). Подробная информация о количестве районов и участков, принадлежащих к аномальным кластерам, приведена в таблице А1 Приложения А. В Москве и Московской области заметно преобладание синих точек, указывающих на заниженные местные средние показатели по сравнению с глобальным средним.
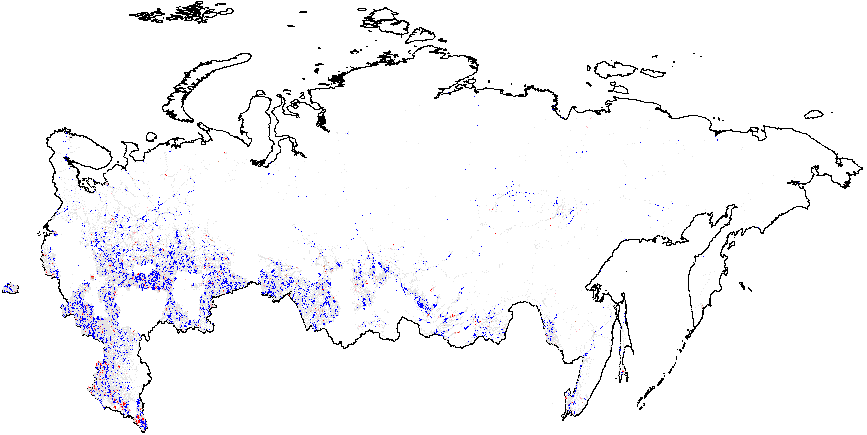
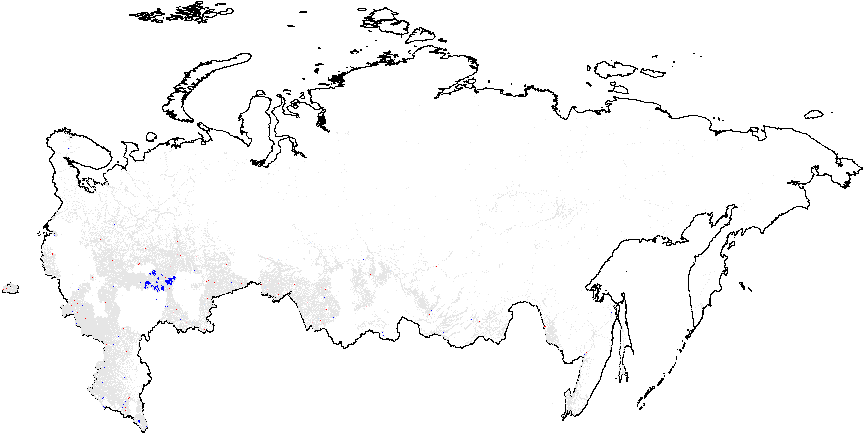
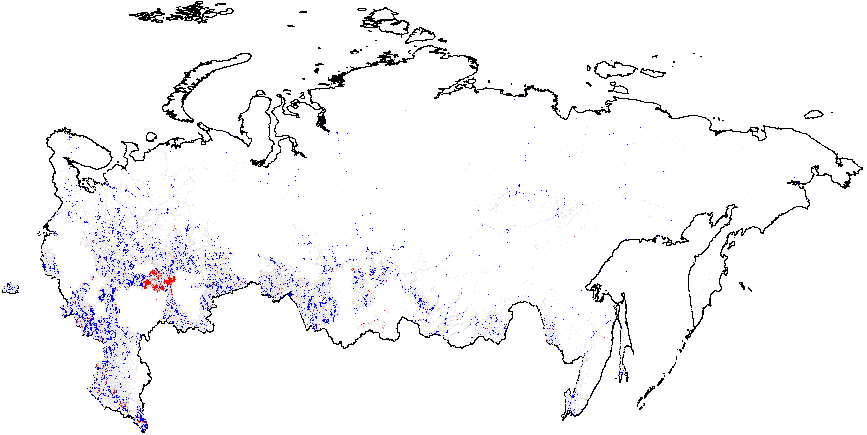
Рисунок 1 (b) иллюстрирует кластеры предельной фальсификации, находящиеся на территории Чечни и северной части Дагестана, а также в Татарстане, со значительным превышением глобального среднего. Хотя на рисунке 1(с) при сравнении с глобальным средним значением \(\overline{CL}=4.48\) не просматриваются доказательства локализованных аномалий в числах голосов за Путина {CL}, на рисунке 1(d) показаны рассеянные на синем фоне красные вкрапления сочетающиеся со сгустками в северной части Дагестана (все это по сравнению с глобальным средним значением \(\overline{P05}=0.21\)). Аномалии в явке показывают похожие результаты. На рисунке 1(e) в границах Татарстана заметен небольшой синий кластер. Однако нужно иметь в виду, что на рисунке 1 завышенное значение глобального среднего говорит о распространенности связанных с явкой аномалий. В этом смысле Татарстан выглядит необычно «сдутым». Наконец, рисунок 1(f) показывает, что красные сигнальные паттерны, превышающие глобальное среднее значение \(\overline{P05}=0.22\), находятся на территории Татарстана и южного Дагестана.
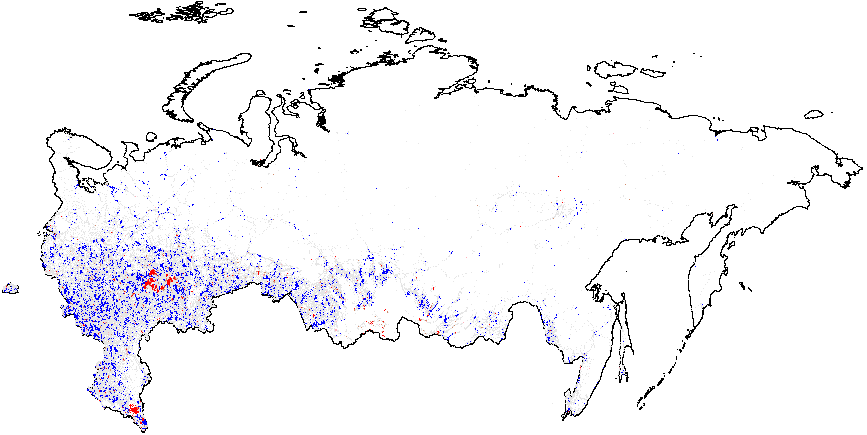
Проанализированные нами данные за 2011 г. показывают, что географические паттерны для двух выборов удивительно согласованы (см. рисунок А2 в Приложении А).
Как мы ранее предполагали, в разные годы кластерные паттерны расположены в подгруппе перечисленных регионов, таких как Дагестан, Татарстан, Белгородская область, Башкортостан, Северная Осетия, Кабардино-Балкария, Мордовия и, наконец, Чечня. Для нескольких регионов оценки конечной смешанной модели находятся в некотором рассогласовании с оценками индекса демократизации, эти регионы – Чувашская Республика и Воронежская область. Карты для конечной смешанной модели также демонстрируют рассеянные крошечные кластеры, скорее всего, объясняющиеся наличием местных политических машин.
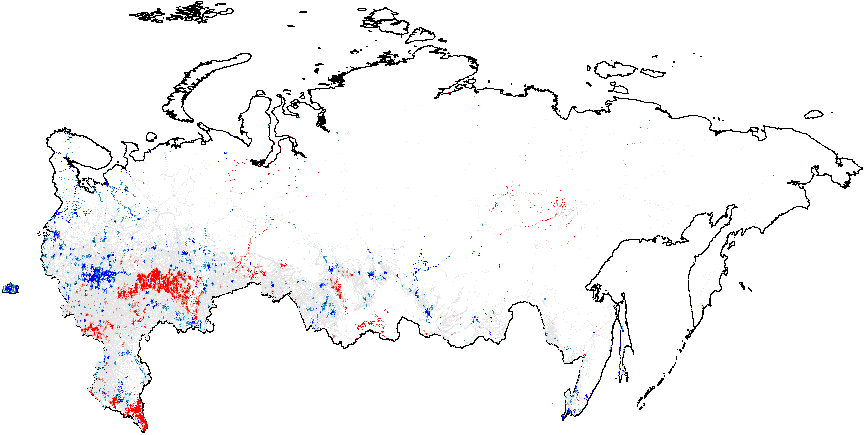
Рисунок 1: Анализ «горячих точек» и изолированных кластеров для различных методов электоральной диагностики, Россия 2012 г., Getis-Ord \(G_i\), данные на уровне участков. Показатели аномалий: {P05} – число “0” и “5” в последней цифре процентов явки и голосах, отданных за действующую власть; {CL} – последние цифры в числах явки и голосах, отданных за действующую власть. Общие средние вероятности фальсификации указаны в скобках. (a) – \(f_i\) (0,08);
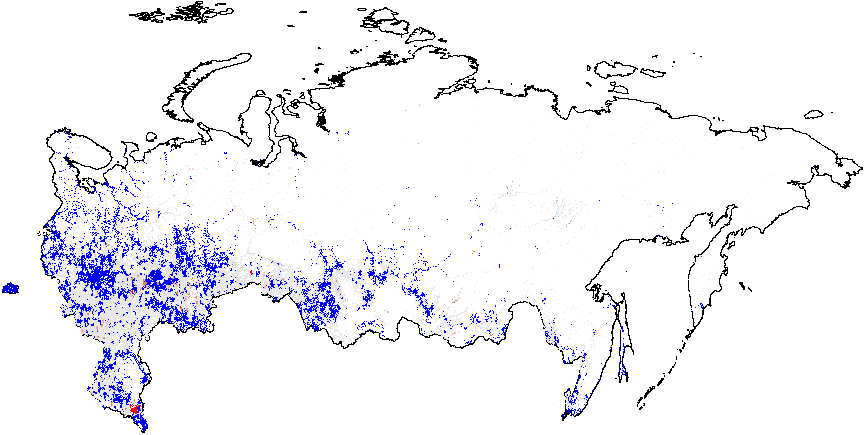
(b) – \(f_e\) (0,002);
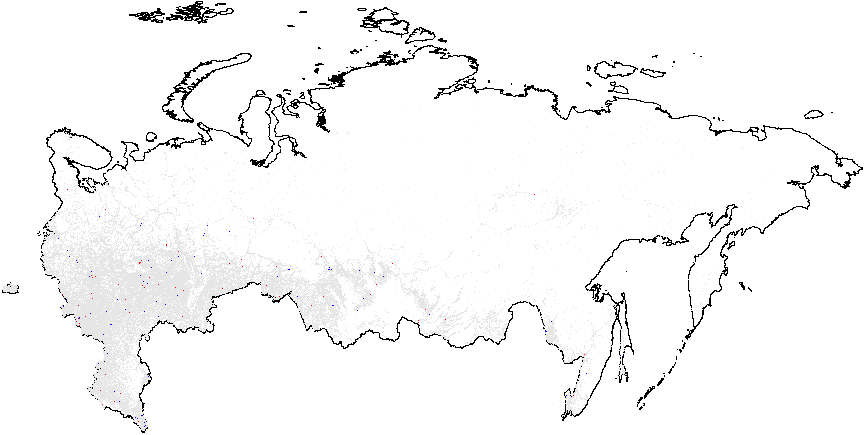
(c) – Путин {CL} (4.48);
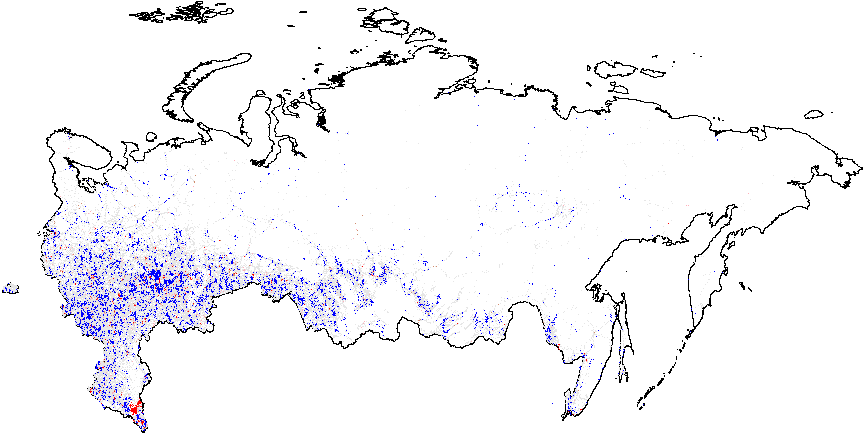
(d) – Путин {P05} (0,21);
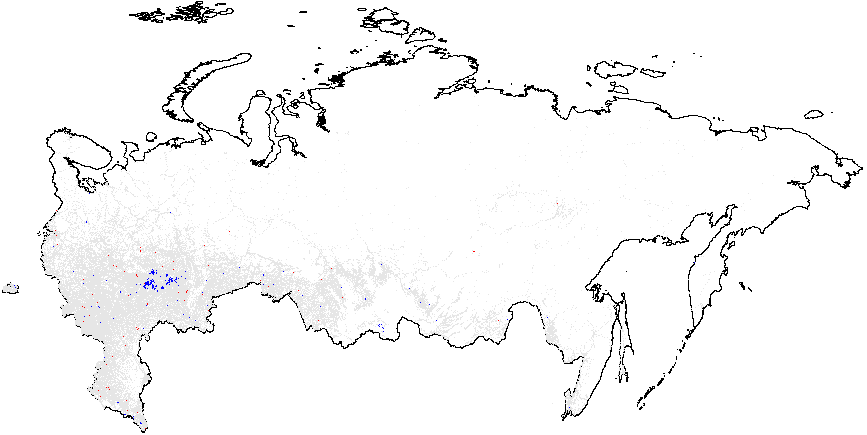
(e) – явка {CL} (4.939);
(f) – явка {P05} (0,22).
Следующий вопрос связан с проверкой степени согласованности между кластерами выстроенных на основе различных оценок: при наличии эмпирической связи между ними можно говорить о существовании сигнальной составляющей в оценках смешанной модели [23]. На рисунке 2 (a), (b) представлены корреляционные матрицы между соответствующими географическими значениями. Категориальная переменная была закодирована через присвоение каждой из категорий участков отдельного числового кода. В кластерном анализе мы имеем дело с четырьмя основными категориями избирательных участков: «ВВ» – высокое значение среди высоких значений аномалий; «LL» – низкое значение среди низких значений аномалий; «LH» – низкое значение среди высоких значений аномалий; «HL» – высокое значение среди низких значений аномалий), измеренное при уровнях значимости \(\alpha\) = 0,01 или \(\alpha\) = 0,05. Полученная категориальная переменная, использованная в нашем корреляционном анализе, была закодирована как «-2» - LL, «- 1» - HL, «0» - незначительная, «1» - LH и «2» - HH. Обоснование построения шкалы переменной, начинающейся с низкого значения кластера среди низких значений и заканчивающейся высоким значением среди высоких значений, сводится к отображению относительной силы кластеризации в разрезе участков.
В отношении обоих выборов, как показывают наши результаты, особенно сильны корреляции между кластерами, связанные с сигнальными паттернами {P05} чисел голосов за Путина/«Единую Россию» и сигнальными паттернами явки {P05} (\(\rho\) = 0,86 для выборов 2011 г., \(\rho\) = 0,91 для выборов 2012 г.) с одной стороны, и показателями инкрементной фальсификации \(f_i\), а также предельной фальсификации \(f_e\) с другой стороны (\(\rho\) = 0,67 для выборов 2011 г., \(\rho\) = 0,77 для выборов 2012 г.). В то время как наблюдается умеренная корреляция между кластерами для предельной фальсификации и кластерами {P05} для явки (\(\rho\) = 0,41 для выборов 2011 г., \(\rho\) = 0,45 для выборов 2012 г.), а также предельной фальсификацией и уровнем поддержки «ЕР»/Путина \(\rho\) = 0,42 для выборов 2011 г., \(\rho\) = 0,46 для выборов 2012 г.), сохраняется довольно слабая корреляция между инкрементной фальсификацией и нашим индикатором {P05} уровня поддержки «ЕР»/Путина (\(\rho\) = 0,28 для выборов 2011 г., \(\rho\) = 0,29 для выборов 2012 г.), а также уровня явки (\(\rho\) = 0,27 для выборов 2011 г., \(\rho\) = 0,25 для выборов 2012 г.). Это наблюдение говорит, скорее всего, о связи географического распределения оценок конечной смешанной модели с силой региональных политических машин. Данный вывод подтверждается в том числе экспертными оценками: список регионов с наименьшим индексом демократичности и наиболее развитыми политическими машинами частично совпадает с кластерами вероятностей фальсификаций, взятыми из конечной смешанной модели.
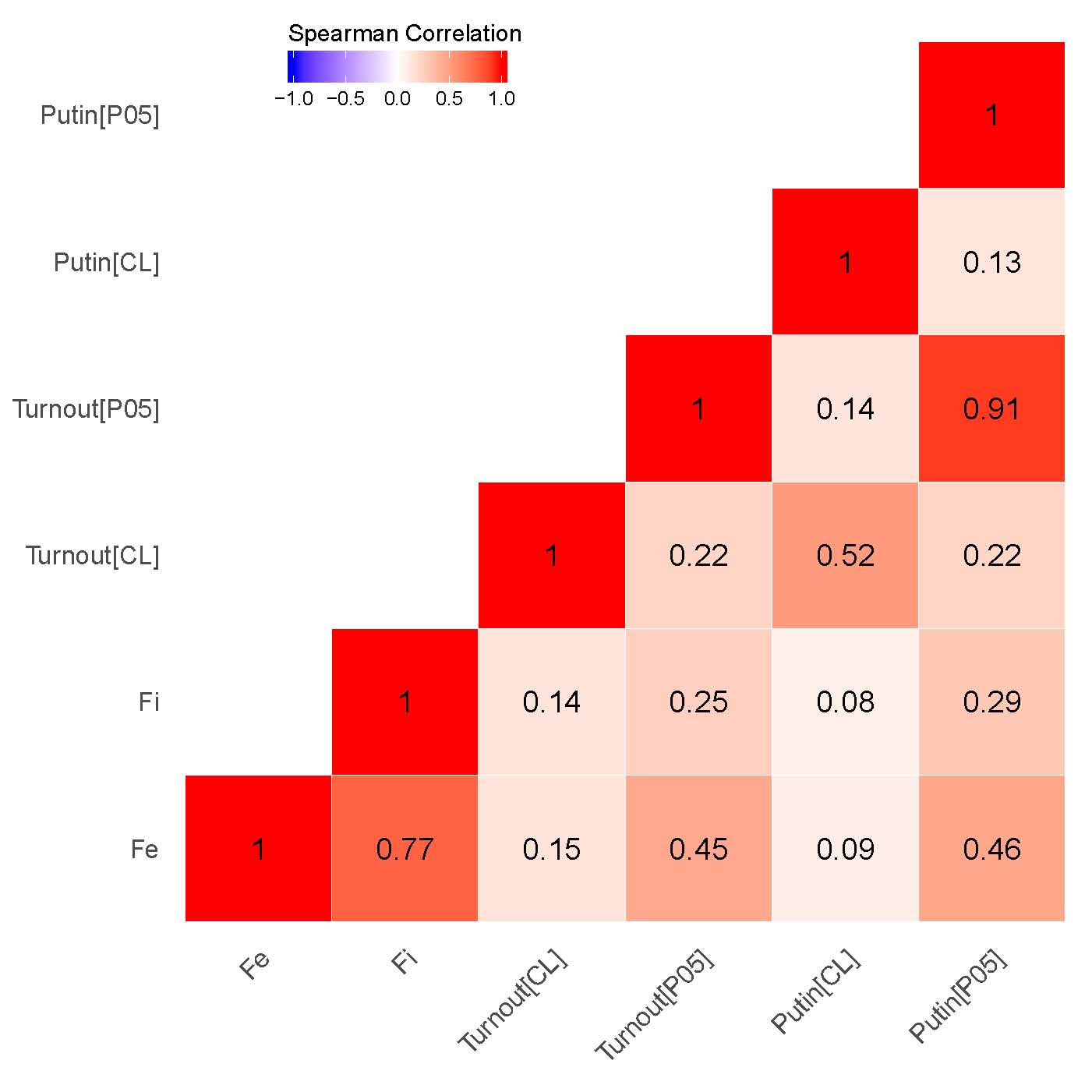
Рисунок 2: Корреляционные матрицы для данных на уровне участков, Getis-Ord \(G_i\). (a) – президентские выборы 2012 г.;
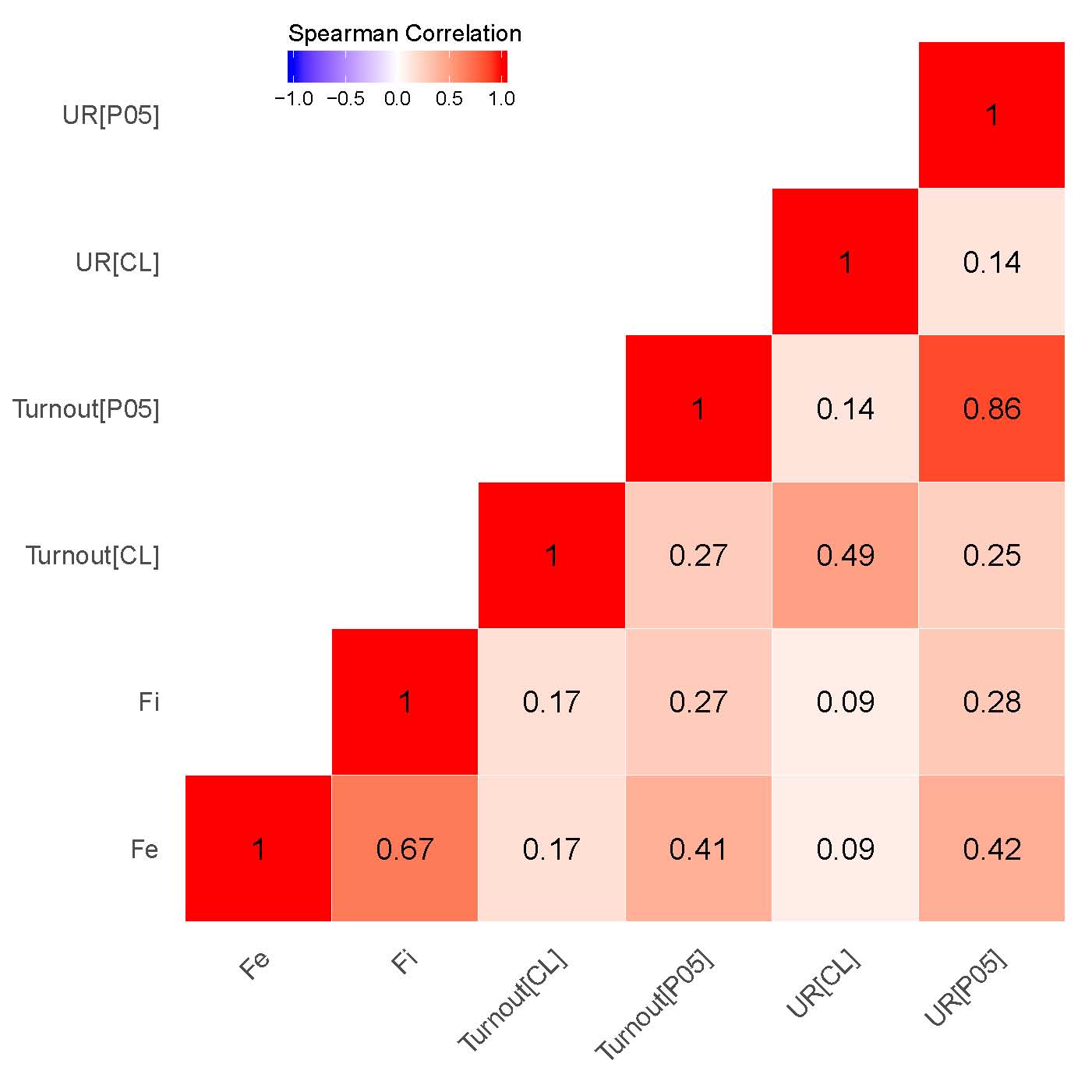
(б) – парламентские выборы 2011 г.
Для анализа горячих точек на субрегиональном административном уровне рассчитываются средние значения оценочных показателей выборов на уровне избирательных участков для каждого района. Подобный подход позволяет проверить, соотносятся ли кластеры районного уровня с кластерами на уровне участков. Мы намеренно представляем карту западной части России для конечных смешанных оценок, исключая из анализа районы с низкой плотностью населения.
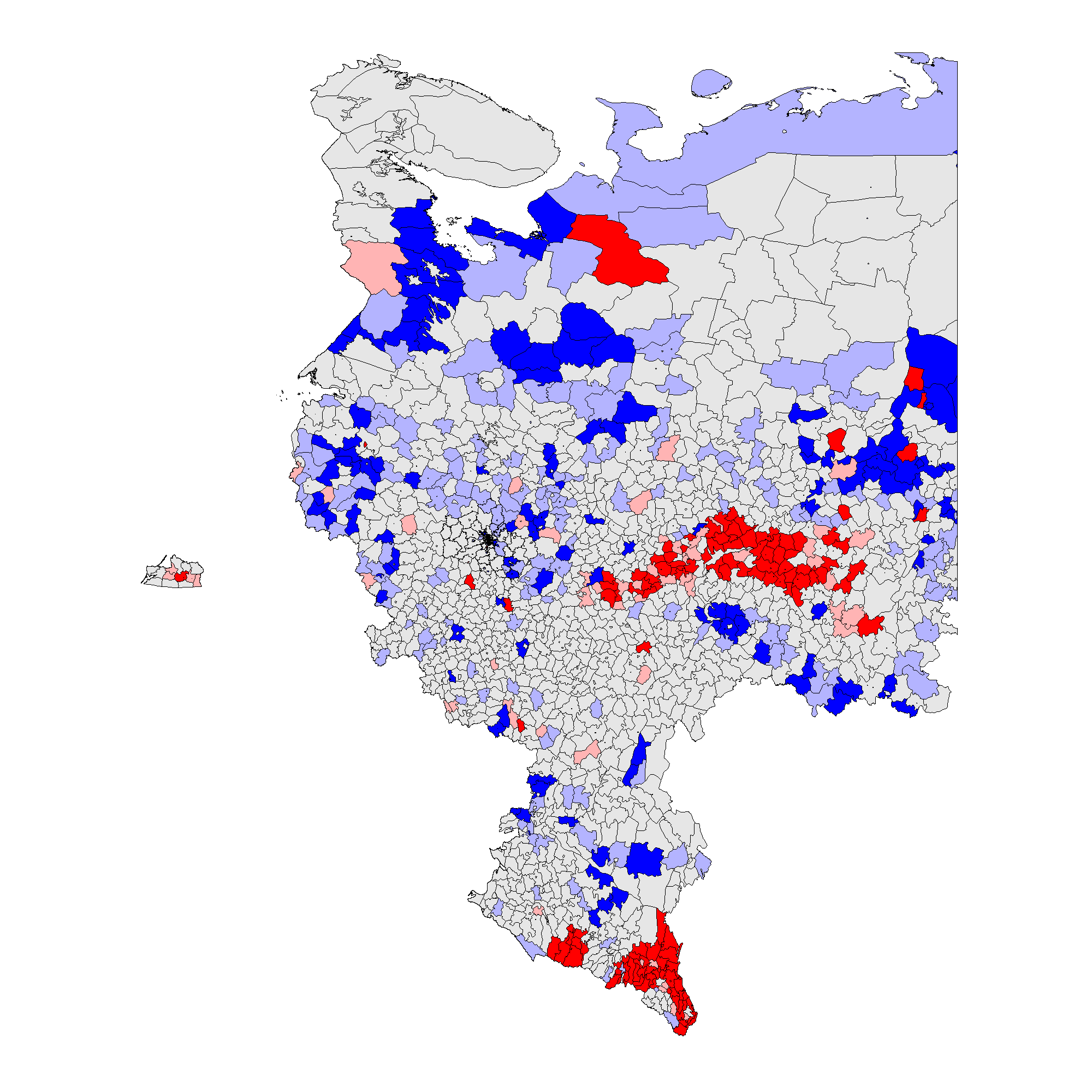
Рисунок 3: Кластерный анализ, локальный индекс Морана \(I_i\), уровень районов. Глобальные средние значения вероятности фальсификации указаны в скобках. (a) – \(f_i\) 2012 (0,09);
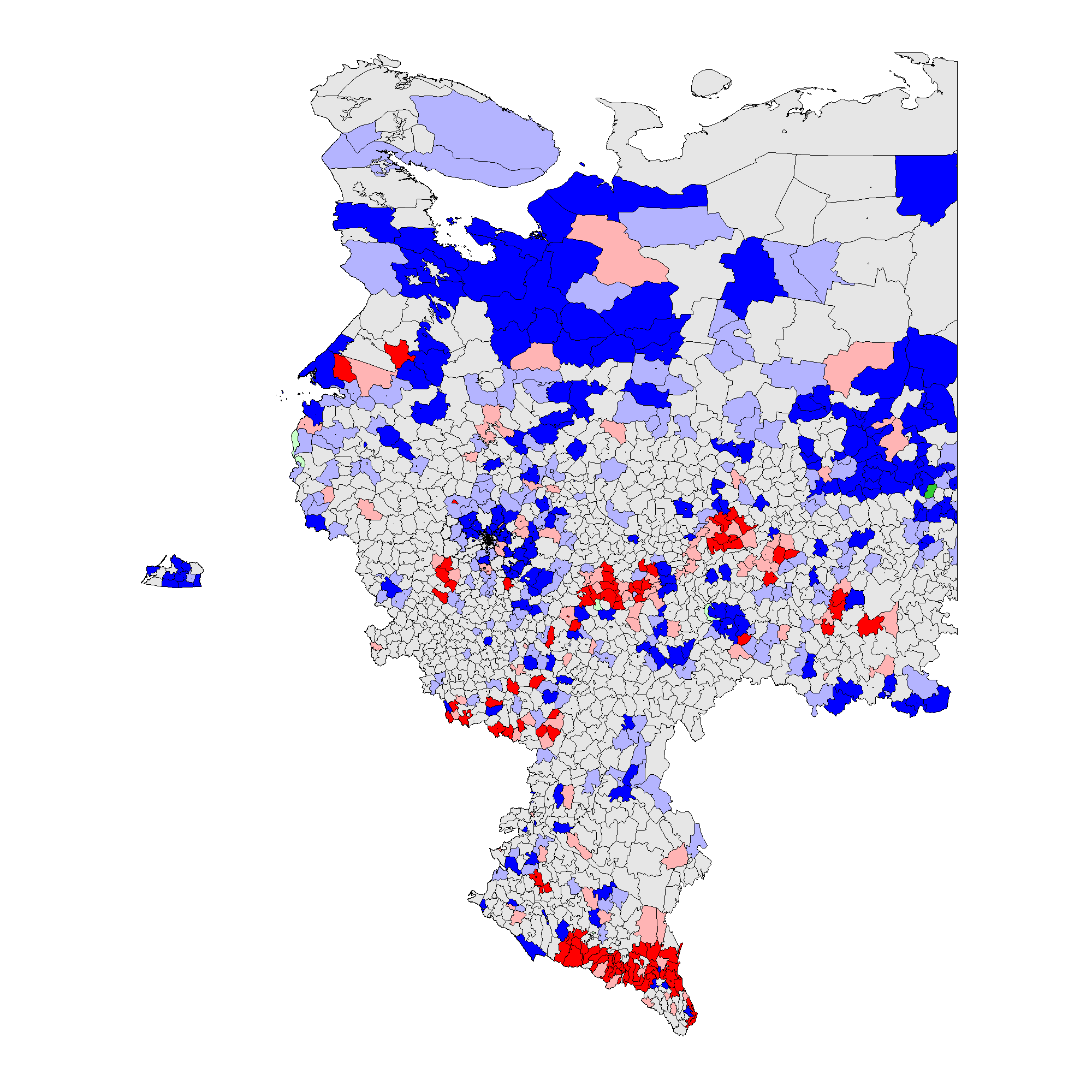
(b) – \(f_i\) 2011(0,13);
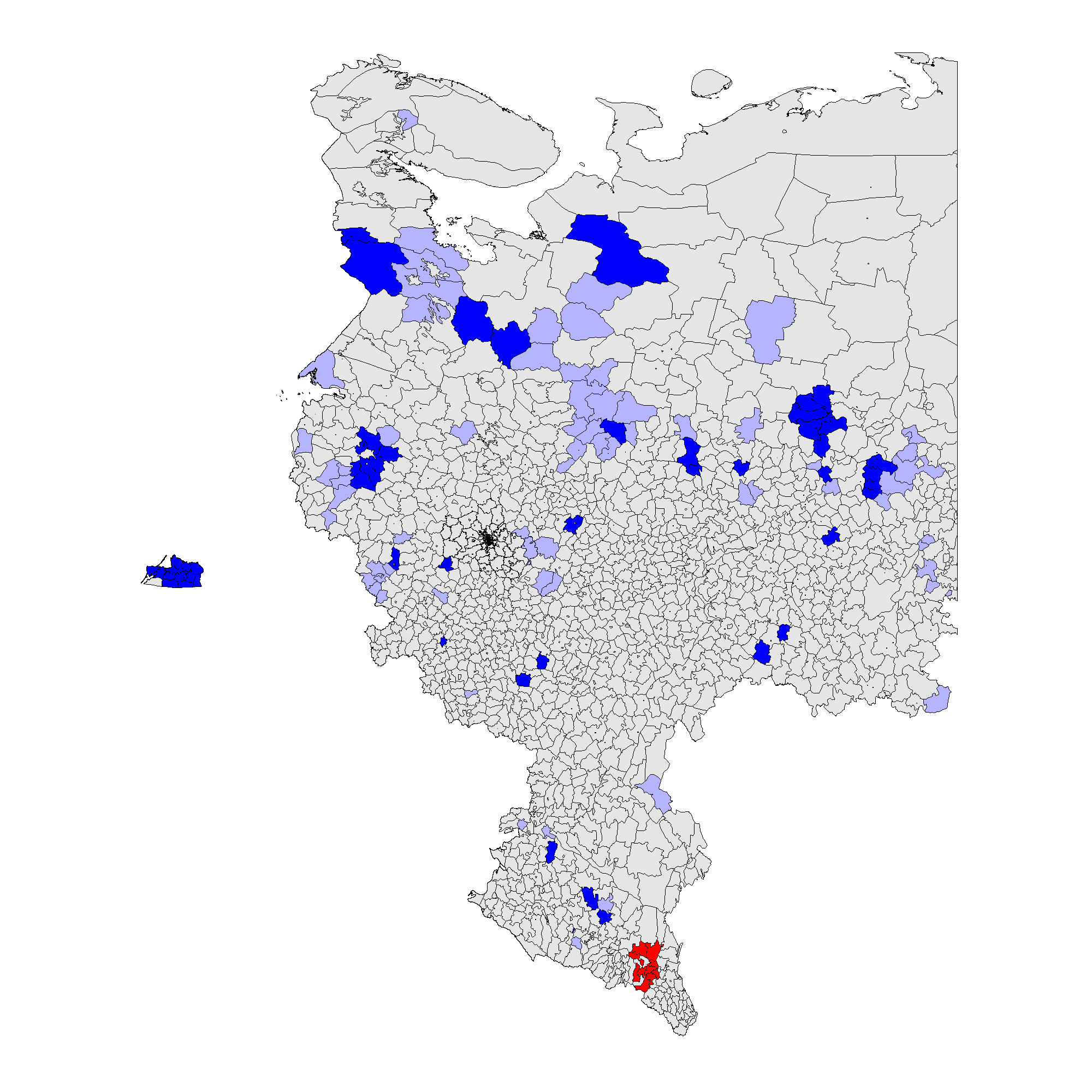
(c) – \(f_e\) 2012 (0,002);
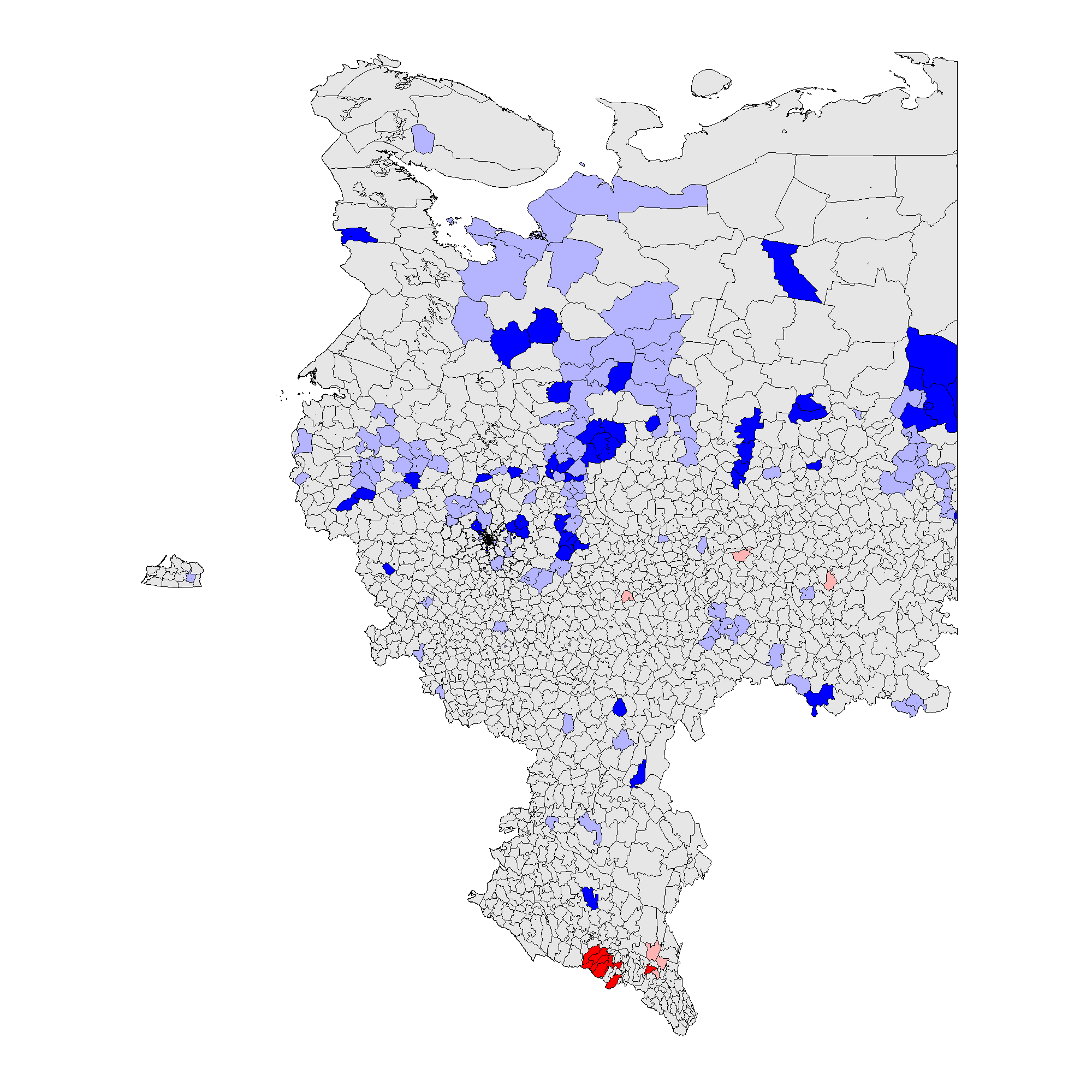
(d) – \(f_e\) 2011 (0,003).
Рисунок 3 показывает, что паттерны кластеров на районном уровне совпадают с паттернами на уровне участков. В 2012 г. кластеры инкрементных фальсификаций \(f_i\) устойчиво преобладали в этнических районах Татарстана, Башкортостана, Мордовии, Чувашии, Дагестана, Чечни, Северной Осетии, и предельных фальсификаций \(f_e\) – в Чечне и Дагестане. В 2011 г. кластеры инкрементных фальсификаций \(f_i\) оказались широко разбросаны, включив в дополнение к ранее упомянутым регионам Амурскую, Белгородскую, Воронежскую области, Краснодарский край, Карачаево-Черкесию и ряд других. Предельные фальсификации \(f_e\) также преобладали на севере Чеченской Республики и Республики Дагестан. Поскольку глобальное среднее значение для выборов 2011 г. выше 2012 г., можно говорить о наличии меньшей гетерогенности для более высоких уровней электоральных аномалий. Для получения дополнительной информации о количестве районов и участков, входящих в аномальные кластеры, см. таблицу A1 в Приложении A.
Таким образом, принимая во внимание совокупность сделанных наблюдений, Гипотеза 2 частично подтверждается нашим эмпирическим анализом: действительно, можно говорить о существовании кластеров электоральных фальсификаций, расположенных в районах, демонстрирующих низкий уровень демократичности и наличие сильных политических машин, в национальных республиках и сельских районах.
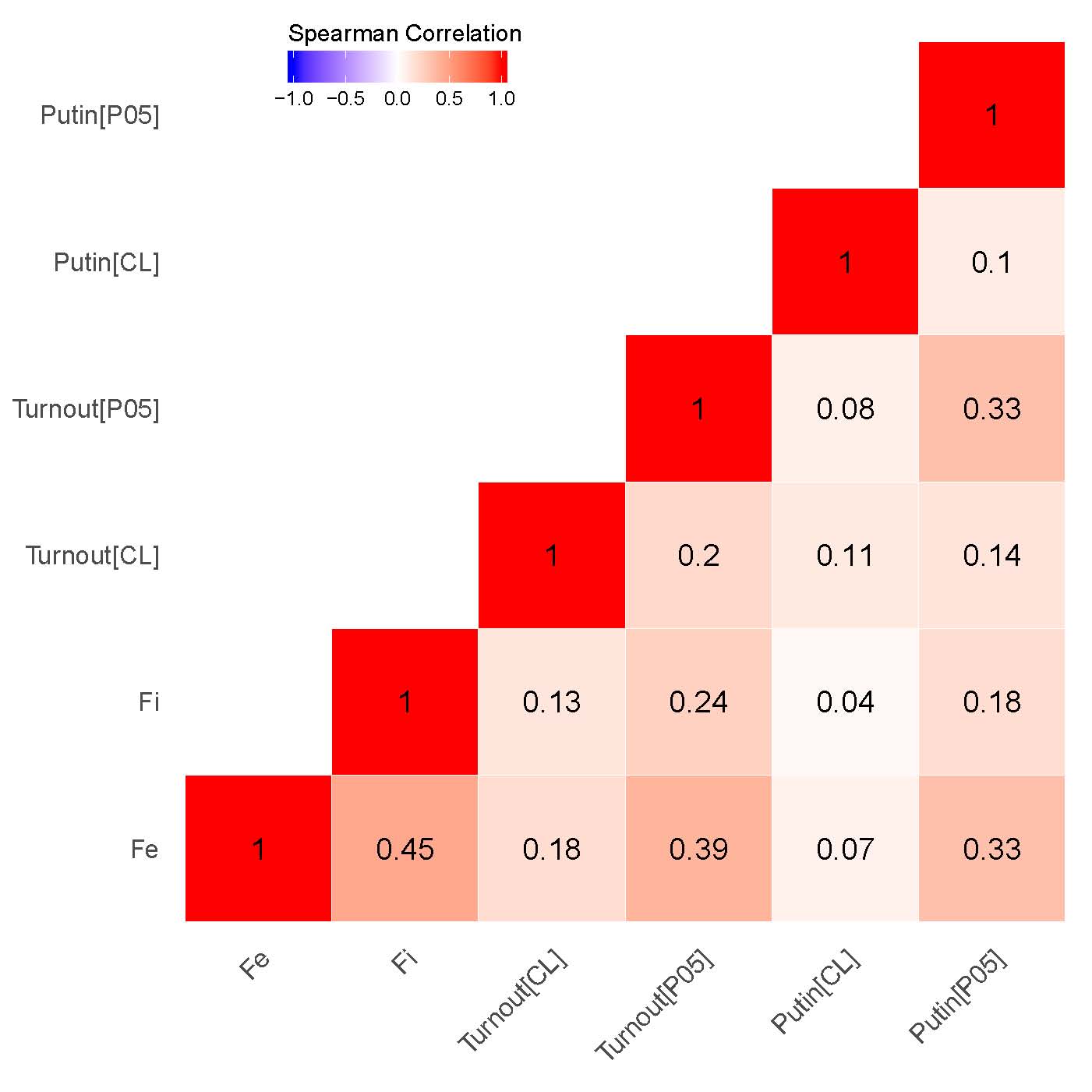
Рисунок 4: Корреляционные матрицы, уровень районов, локальный индекс Морана \(I_i\). (a) – президентские выборы 2012 г.;
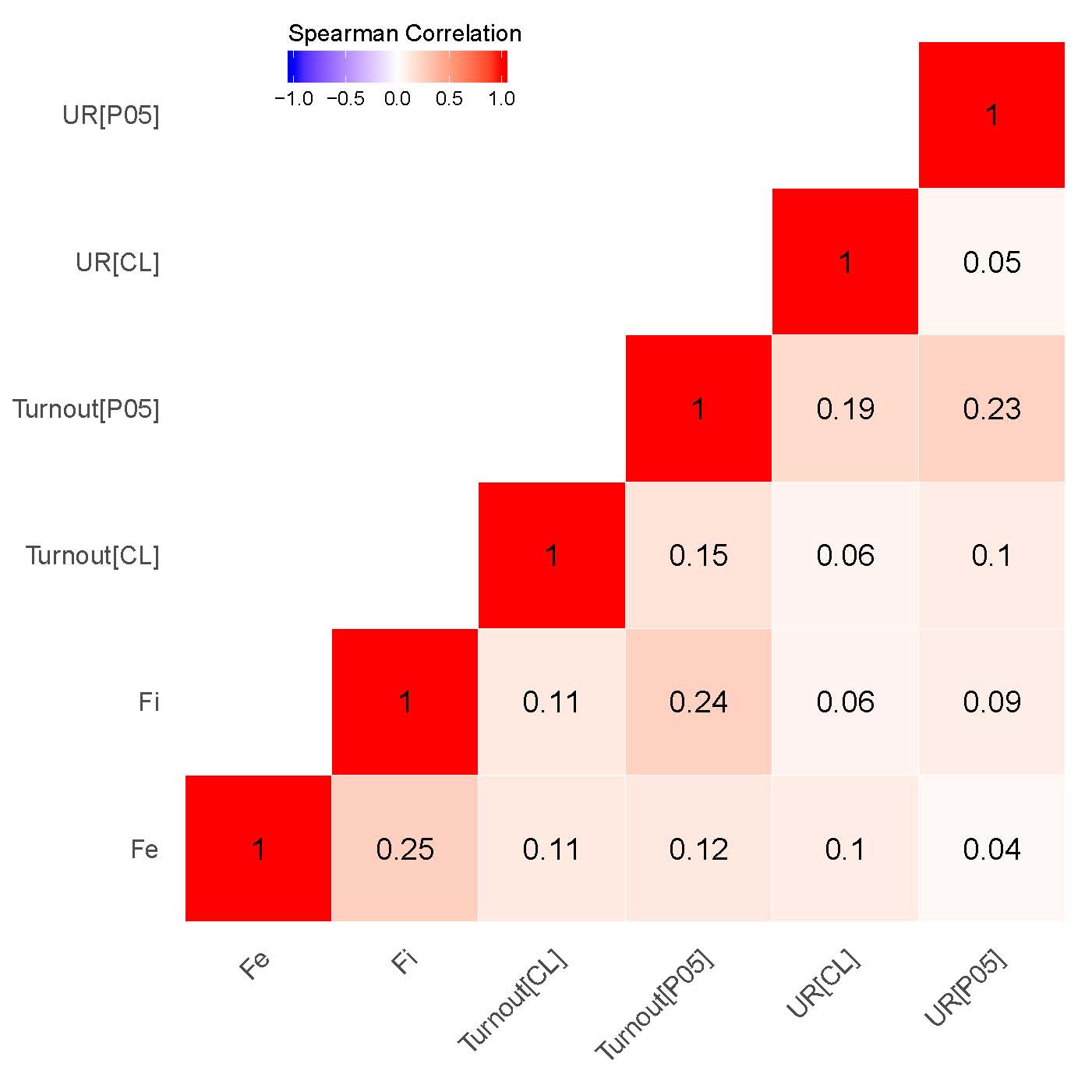
(б) – парламентские выборы 2011 г.
Не удивительно, что корреляционные матрицы, построенные с использованием данных районного уровня, демонстрируют несколько более слабые выводы по сравнению с корреляционными матрицами для участков. Примечательно, что корреляции между представляющими интерес переменными по президентским выборам сильнее по сравнению с парламентскими выборами. Обе оценки конечной смешанной модели слабо или умеренно коррелируют между собой (\(\rho\) = 0,25 для выборов 2011 г., \(\rho\) = 0,45 для выборов 2012 г.) и сигнальным индикатором {P05} (\(f_i\): \(\rho\) = 0,24 для выборов 2011 г., \(\rho\) = 0,24 для выборов 2012 г.; \(f_e\): \(\rho\) = 0,12 для выборов 2011 г., \(\rho\) = 0,39 для выборов 2012 г.). Умеренная корреляция, по-видимому, наблюдается в 2012 г. между оценками, измеряющими сигнальные паттерны {P05} для явки и поддержки Путина (\(\rho\) = 0,33).
Таким образом, представленный кластерный анализ говорит о том, что некоторые паттерны полученные из конечной смешанной модели, могут хорошо описываться тестом последних цифр. Наблюдаемая корреляция между оценками конечной смешанной модели и результатами цифровых тестов {P05} выражена умеренно сильно в зависимости от уровня агрегирования данных. Более того, аномалии на уровне районов, похоже, довольно хорошо воспроизводят аномалии на уровне участков. Это интересное наблюдение позволяет сделать два важных вывода. Во-первых, в отношении механизма фальсификаций можно говорить об организации и координации фальсификаций на более высоких уровнях. Во-вторых, отсутствие точной географической информации об избирательных участках, а именно – отсутствие координат участков, не обязательно препятствует проведению кластерного анализа на более высоком уровне; степень фальсификации выборов на уровне избирательных участков прослеживается и на районном уровне.
Таким образом, наш эмпирический анализ подтверждает Гипотезу 3: в зависимости от избирательного контекста на различных уровнях наблюдаются умеренные или сильные корреляции между географическими кластерами оценок конечной смешанной модели и географическими кластерами оценок других методов электоральной диагностики, связанных с сигнальными паттернами ({P05} тест для явки и голосования за действующую власть), а также аномальными последними цифрами в итогах голосования {CL}. Отсюда можно сделать вывод, что оценки, полученные из конечной смешанной модели, могут относиться к возможностями региональных руководителей в мобилизации соответствующих политических машин, нацеленных на обеспечение кремлёвского кандидата или партии власти необходимой электоральной поддержкой.
7. Заключение
Несмотря на то, что никакие методы электоральной диагностики не могут служить окончательным доказательством фальсификаций, сочетание данных наблюдателей и избирательных технологий, а также разнообразных методов электоральной диагностики позволяет с большей долей уверенности говорить об их существовании. Данное исследование было нацелено на валидационную проверку инновационного инструмента электоральной диагностики, а именно – конечной смешанной модели, с привлечением альтернативных данных наблюдателей, новых технологий голосования и нескольких методов электоральной диагностики, чувствительных к «машинной политике» в регионах и на местах. Все три гипотезы были полностью или частично подтверждены в ходе проведённого анализа данных. Новый метод укрепил наши ожидания в том, что фальсификации присутствуют на избирательных участках, где используются обычные урны для голосования, и нет хорошо подготовленных наблюдателей. Использование КЭГ в отдаленных районах, лишенных надлежащего наблюдения за выборами, сопряжено с повышенной вероятностью фальсификаций – конечная смешанная модель это точно улавливает.
Географический кластерный анализ показывает наличие кластеров, в основном расположенных в регионах с низким уровнем демократичности и сильными политическими машинами – как правило, это этнические республики и сельские районы. Кроме того, можно сделать вывод о том, что рассмотренные нами тесты для последних цифр относительно точно предсказывают образование географических кластеров, выстроенных на оценках смешанной модели.
Таким образом, на сегодняшний день разработка конечной смешанной модели как части «Инструментария электоральной диагностики» (Election Forensics Toolkit) представляется очень перспективным проектом, безусловно требующим своей дополнительной верификации в разнообразных избирательных, политических и социокультурных контекстах.
Приложение. Таблицы и рисунки

Рисунок A1: (а) КЭГ

(b) КОИБ.
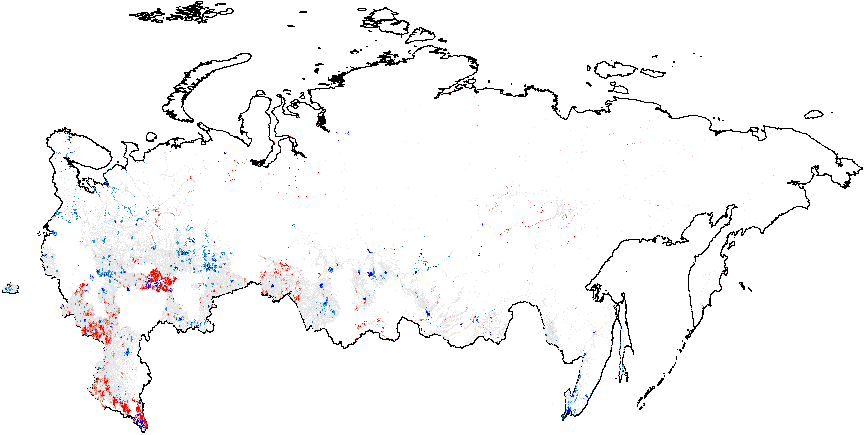
Рисунок A2: Кластерный анализ индикаторов электоральной диагностики, Россия, 2011, Getis-Ord \(G_i\), данные уровня участка. Поскольку некоторые из регионов изменили номера своих избирательных участков в 2012 г., (по которым есть геоданные) по сравнению с 2011 г., (для которых нет геоданных), эти регионы были удалены из кластерного анализа. В результате удалённые области отображаются в виде пустых мест на картах 2011 г. Показатели аномалий: {P05} – число “0” и “5” в последней цифре процентов явки и голосах, отданных за действующую власть; {CL} – последние цифры в числах явки и голосах, отданных за действующую власть. Общие средние показатели вероятности фальсификаций указаны в скобках. (a) – \(f_i\) (0.11);
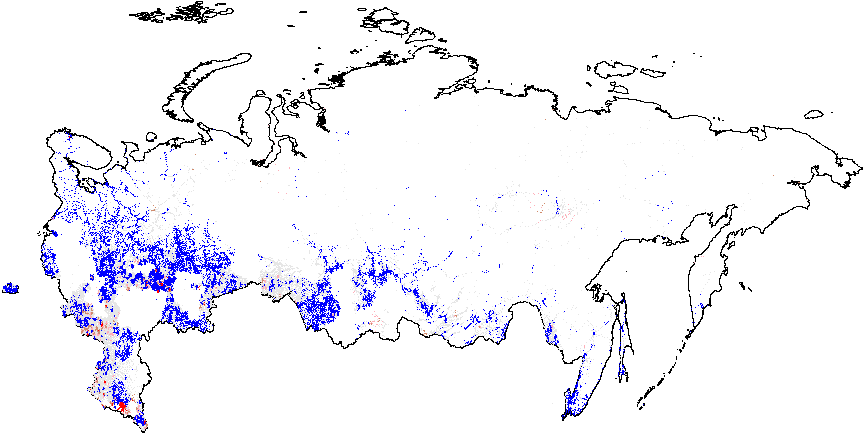
(b) – \(f_e\) (0.002);
(c) – UR{CL} (4.47);
(d) – UR{P05} (0.21);
(e) – Явка {CL} (4.92);
(f) – Явка {P05} (0.22).
Таблица A1: Количество районов и участков в аномальных кластерах (красные пятна) по регионам
| Регион | Президентские выборы | Парламентские выборы | |||||||
| Участки | Районы | Участки | Районы | ||||||
 |
 |
 |
 |
 |
 |
 |
 |
||
| Амурская область | 3 | ||||||||
| Белгородская область | 4 | 171 | 2 | 17 | 280 | 14 | |||
| Брянская область | 7 | 11 | |||||||
| Республика Чечня | 95 | 154 | 12 | 14 | 12 | 14 | |||
| Челябинская область | 9 | 38 | |||||||
| Чукотский автономный округ | 1 | ||||||||
| Республика Чувашия | 8 | 306 | 9 | 2 | 24 | 2 | |||
| Город Москва | 3 | ||||||||
| Иркутская область | 3 | ||||||||
| Республика Кабардино-Балкария | 162 | 179 | 8 | ||||||
| Калужская область | 17 | 53 | 3 | ||||||
| Республика Карачаево-Черкесия | 111 | 9 | 23 | 133 | 9 | ||||
| Кемеровская область | 2 | 189 | 5 | ||||||
| Хабаровский край | 1 | ||||||||
| Ханты-Мансийский автономный округ | 13 | 1 | |||||||
| Кировская область | 3 | ||||||||
| Костромская область | 1 | ||||||||
Таблица показана не полностью Открыть полностью
Поступила в редакцию 25.04.2018, в окончательном виде 01.10.2018.
Список литературы
- Anselin L. Local Indicators of Spatial Association. – LISA. Geographical Analysis. 1995. V. 27. No. 2. P. 93–115.
- Bader M. Do New Voting Technologies Prevent Fraud? Evidence from Russia. – The USENIX Journal of Election Technology and Systems. 2013. V. 2. No. 1. P. 1–18.
- Beber B., Scacco A. What the Numbers Say: A Digit-Based Test for Election Fraud. – Political Analysis. 2012. V. 20. No. 2. P. 211–234.
- Beber B., Scacco A. What the Numbers Say: A Digit-Based Test for Election Fraud Using New Data from Nigeria. August 2008.
- Bjornlund E.C. Beyond Free and Fair: Monitoring Elections and Building Democracy. Woodrow Wilson Center Press, 2004.
- Cantu F., Saiegh S.M. Fraudulent Democracy? An Analysis of Argentina’s Infamous Decade Using Supervised Machine Learning. – Political Analysis. 2011. V. 19. No. 4. P. 409–433.
- Darr B., Hesli V. Differential Voter Turnout in a Post-Communist Muslim Society: The Case of Kyrgyz Republic. – Communist and Post-Communist Studies. 2010. V. 43. No. 3. P. 309–324.
- Deckert J., Myagkov M., Ordeshook P.C. Benford’s Law and the Detection of Election Fraud. – Political Analysis. 2011. V. 19. No. 3. P. 245–268.
- Enikolopov R., Korovkin V., Petrova M., Sonin K., Zakharov A. Field Experiment Estimate of Electoral Fraud in Russian Parliamentary Elections. – Proceedings of the National Academy of Sciences of the United States of America. 2013. V. 110. No. 2. P. 448–452.
- Estok M., Nevitte N., Cowan G. The Quick Count and Election Observation: An NDI Guide for Civic Organizations and Political Parties. Technical report, National Democratic Institute for International Affairs, 2002.
- Golosov G.V. Disproportionality by Proportional Design: Seats and Votes in Russia’s Regional Legislative Elections, December 2003–March 2005. – Europe-Asia Strudies. 2006. V. 58. No. 1. P. 25–55.
- Golosov G.V. Machine Politics: the Concept and Its Implications for Post-Soviet Studies. – Demokratizatsiya. 2013. V. 21. No. 4. P. 459–480.
- Greene K.F. Why Dominant Parties Lose. Mexico’s Democratization in Comparative Perspective. Cambridge University Press, 2007.
- Hale H.E. Correlates of Clientilism: Political Economy, Politicized Ethnicity, and PostCommunist Transition. – Patrons, Clients and Policies: Patterns of Democratic Accountability and Political Competition / Kitschelt H., Wilkinson S.I., eds. New York: Cambridge University Press, 2007. P. 227–250.
- Hale H.E. Explaining Machine Politics in Russia’s Regions: Economy, Ethnicity, and Legacy. – Post-Soviet Affairs. 2003. V. 19. No. 3. P. 228–263.
- Herron E.S. Elections and Democracy After Communism? New York: Palgrave Macmillan, 2009.
- Herron E.S. The Effect of Passive Observation Methods on Azerbaijan’s 2008 Presidential Election and 2009 Referendum. – Electoral Studies. 2010. V. 29. P. 417–424.
- Hicken A., Mebane, W.R., Jr. A Guide to Election Forensics. Working paper for IIE/USAID subaward #DFG-10-APS-UM, “Development of an Election Forensics Toolkit: Using Subnational Data to Detect Anomalies”, 2015.
- Hyde S.D. Election Fraud: Detecting and Deterring Electoral Manipulation. Washington, DC: Brookings Institution Press, 2008. P. 201–215.
- Hyde S.D. The Observer Effect in International Politics: Evidence from a Natural Experiment. – World Politics. 2007. V. 60. P. 37–63.
- Hyde S.D. The Pseudo-Democrats Dilemma: Why Election Monitoring Became an International Norm. Cornell University Press, 2011.
- Ichino N., Schundeln M. Deterring or Displacing Electoral Irregularities? Spillover Effects of Observers in a Randomized Field Experiment in Ghana. – The Journal of Politics. 2012. V. 74. No. 1. P. 292–307.
- Kalinin K., Mebane W.R., Jr. Understanding Electoral Frauds through Evolution of Russian Federalism: the Emergence of Signaling Loyalty. Paper prepared for the Annual Meeting of Midwest Political Science Association. Chicago, March 2013.
- Kalinin K., Mebane W.R., Jr. Worst Election Ever in Russia? Prepared for presentation at the 2017 Annual Meeting of the Midwest Political Science Association. Chicago, April 2017.
- Kelley J. Monitoring Democracy: When International Election Observation Works and Why it Often Fails. Princeton: Princeton University Press, 2012.
- Klimek P., Yegorov Y., Hanel R., Thurner S. Statistical Detection of Systematic Election Irregularities. – Proceedings of the National Academy of Sciences of the United States of America. 2012. V. 109. No. 41. P. 16469–16473.
- Kobak D., Shpilkin S., Pshenichnikov M.S. Statistical Anomalies in 2011-2012 Russian Elections Revealed by 2D Correlation Analysis. May 2012.
- Kuenzi M., Lambright G.M. Who Votes in Africa? An Examination of Electoral Participation in 10 African Countries. – Party Politics. 2011. V. 17. No. 6. P. 767–799.
- Magaloni B. Voting for Autocracy: Hegemonic Party Survival and its Demise in Mexico. Cambridge Studies in Comparative Politics, 2006.
- Matsuzato K. Progressive North, Conservative South? Reading the Regional Elite as a Key to Russian Electoral Puzzles. In Regions: A Prism to View the Slavic Eurasian World. Sapporo: Slavic Research Center, 2000.
- McLachlan G., Peel D. Finite Mixture Models. New York: Wiley, 2000.
- Mebane W.R., Jr. Comment on “Benford’s Law and the Detection of Election Fraud”. – Political Analysis. 2011. V. 19. No. 3. P. 269–272.
- Mebane W.R., Jr. Election Forensics: Frauds Tests and Observation-level Frauds Probabilities. Prepared for presentation at the 2016 Annual Meeting of the Midwest Political Science Association, Chicago, April 7–10, 2016.
- Mebane W.R., Jr. Election Forensics: Vote Counts and Benford’s Law. Paper prepared for the 2006 Summer Meeting of the Political Methodology Society, UC-Davis, July 20-22, 2006.
- Mebane W.R., Jr. Election Fraud or Strategic Voting? 2010.
- Mebane W.R., Jr., Kalinin K. Comparative Election Fraud Detection. Prepared for presentation at the Annual Meeting of the American Political Science Association, Toronto, Canada, Sept. 3-6 2009.
- Mebane W.R., Jr., Klaver J. Election Forensics: Strategies versus Election Frauds in Germany. Prepared for presentation at the 2015 Annual Conference of the European Political Science Association, Vienna, Austria, 2015.
- Mebane W.R., Jr. Second-digit Tests for Voters Election Strategies and Election Fraud. Prepared for presentation at the 2012 Annual Meeting of the Midwest Political Science Association, Chicago, April 12–15, 2012, April 2012.
- Mebane W.R., Jr., Sekhon J.S. Genetic Optimization Using Derivatives: The rgenoud Package for R. – Journal of Statistical Software. 2011. V. 42. No. 11. P. 1–26.
- Myagkov M., Ordeshook P.C., Shakin D. The Forensics of Election Fraud: With Applications to Russia and Ukraine. New York: Cambridge University Press, 2009.
- Norden L.., Burstein A., Hall J.L., Chen M. Post-election Audits: Restoring Trust in Elections. Technical report, Brennan Center for Justice at New York University School of Law, the Samuelson Law, Technology & Public Policy Clinic at the University of California, Berkeley School of Law (Boalt Hall), 2007.
- Ord J.K., Getis A. Local Spatial Autocorrelation Statistics: Distributional Issues and an Application. – Geographical Analysis. 1995. V. 27. P. 286–306.
- Pericchi L.R., Torres D. Quick Anomaly Detection by the Newcomb-Benford Law, with Applications to Electoral Processes Data from the USA, Puerto Rico and Venezuela. – Statistical Science. 2011. V. 26. No. 4. P. 502–516.
- Reisinger W.M., Moraski B.J. The Regional Roots of Russia’s Political Regime. Ann Arbor: University of Michigan Press, 2017.
- Sekhon J.S. Multivariate and Propensity Score Matching Software with Automated Balance Optimization. – Journal of Statistical Software. 2012. V. 42. P. 1–52.
- Simpser A. A Theory of Corrupt Elections. Working paper, 2006.
- Simpser A. Why Governments and Parties Manipulate Elections: Theory, Practice, and Implications. New York: Cambridge University Press, 2013.
- Sjoberg F.M. Autocratic Adaptation: The Strategic Use of Transparency and the Persistence of Election Fraud. – Electoral Studies. 2014. V. 33. P. 233–245.
- Sjoberg F.M. Making Vote Count: Evidence from Field Experiments about the Efficacy of Domestic Election Observation. Harriman Institute Working Paper No. 1, October 2012.
- Solnick S.L. Federal Bargaining in Russia. – East European Constitutional Review. 1995. V. 4. No. 4. P. 52–58.
- Арбатская М. Сколько же в России избирателей? Политико-географический анализ общего числа российских избирателей и уровня их активности. 1990-2004). Иркутск: Институт географии СО РАН, 2004. 300 с.
- Бузин А., Любарев А. Преступление без наказания: Административные технологии федеральных выборов 2007–2008 годов. М.: Никколо М, 2008. 284 с.
- Калинин К., Шпилькин С. Комплексная диагностика фальсификации на российских президентских выборах 2012 года. – Троицкий вариант, 27.03.2012. Доступ: http://trv-science.ru/2012/03/27/shpilkin-kalinin/ (проверено 03.03.2019). - http://trv-science.ru/2012/03/27/shpilkin-kalinin/
- Киреев А. Моя оценка уровня фальсификации на выборах в Госдуму по субъектам федерации. – Livejournal, 09.10.2016. Доступ: http://kireev.livejournal.com/1313935.html (проверено 03.03.2019). - http://kireev.livejournal.com/1313935.html
- Петров, Н., Титков, А. Рейтинг Демократичности Регионов Московского центра Карнеги: 10 лет в строю. Московский центр Карнеги, январь 2013.
- Собянин А., Суховольский В. Демократия, ограниченная фальсификациями: Выборы и референдумы в России в 1991–1993 гг. Москва: Проектная группа по правам человека, 1995. 268 с.
- Шпилькин С. Двугорбая Россия . – Троицкий вариант, 04.10.2016. Доступ: https://trv-science.ru/2016/10/04/dvugorbaya-rossiya/ (проверено 03.03.2019). - https://trv-science.ru/2016/10/04/dvugorbaya-rossiya/
- Шпилькин С. Статистика исследовала выборы: Статистический анализ выборов в Госдуму 2011 года показывает возможные фальсификации. – Gazeta.ru, 10.12.2011. Доступ: https://www.gazeta.ru/science/2011/12/10_a_3922390.shtml (проверено 03.03.2019). - https://www.gazeta.ru/science/2011/12/10_a_3922390.shtml
