Модификация метода Собянина-Суховольского
Аннотация
Для оценки качества выборов по данным протоколов избирательных комиссий об итогах голосования предлагается рассматривать коэффициенты Собянина-Суховольского (коэффициенты линейной интерполяции на плоскости «явка-доля голосов, полученных претендентом») в зависимости от порога отсечения явки после упорядочивания комиссий по явке. Рассмотрены изъяны классического метода Собянина-Суховольского; приведены примеры использования модифицированного метода для изучения реальной электоральной статистики. Этим же методом исследуются компьютерные имитации выборов при наличии территориальных неоднородностей в явке и электоральных предпочтениях, а также эффекты от прямых фальсификаций итогов голосования.
Классический метод Собянина-Суховольского
В книге Собянина А.А. и Суховольского В.Г. «Демократия, ограниченная фальсификациями: Выборы и референдумы в России в 1991-1993 гг.» [5] предложен метод обнаружения фальсификаций на выборах с помощью анализа официальных данных о голосовании (назовем его «методом С-С»). Этот метод заключается в следующем:
1) По протоколам избирательных комиссий (чаще всего используются данные участковых избирательных комиссий, однако можно использовать также данные комиссий более высокого уровня – важно, чтобы исследуемые комиссии были соразмерными по списочному числу избирателей) вычисляются значения:
\(\tau_i, y_{ij}, i = 1, … N; j = 1, … M,\)
где \(\tau_i\) - показатель явки в \(i\)-й комиссии, \(y_{ij}\) - доля избирателей \(i\)-й комиссии, отдавших голос за \(j\)-го претендента (кандидата или избирательное объединение), исчисленная от общего (списочного) числа избирателей в \(i\)-й комиссии;
2) Для победителя \(J\) по точкам \((\tau_i, y_{ij}), i = 1, … N\) вычисляются коэффициенты линейной регрессии \((a_j, b_j)\), где \(a_j\) – коэффициент при первой степени регрессионного уравнения, а \(b_j\) – при нулевой степени.
3) Коэффициент \(a_j\) (будем называть его линейный коэффициент С-С) сравнивается с долей голосов, набранных победителем, исчисленной от числа проголосовавших избирателей \(v_j\). Коэффициент \(b_j\) (будем называть его свободным коэффициентом С-С) сравнивается с нулем.
Если \(a_j\) существенно больше \(v_j\), а \(b_j\) существенно меньше нуля (мы не уточняем, что значит «существенно», поскольку эта оценка субъективна и различается у разных исследователей), то имеются основания подозревать, что результаты были сфальсифицированы одним из следующих способов (или их комбинацией):
А) принуждение к голосованию за победителя тех избирателей, которые не собирались участвовать в голосовании;
Б) голосование за других лиц в пользу победителя;
В) реальный вброс бюллетеней за победителя (в ящики для голосования или непосредственно при подсчете голосов);
Г) фальсификация протокола путем дописывания числа проголосовавших и числа голосов за победителя.
Метод получил довольно широкое распространение и использовался в работах [4; 1; 3], в которых рассмотрены выборы разных уровней в России, Украине, Литве, США, начиная с середины 1990-х гг. и до 2008 г.
Основанием для подозрений в фальсификации является тот факт, что фальсификации А-Г действительно отклоняют коэффициенты С-С в указанную сторону, иначе говоря, эти фальсификации являются достаточными для отклонений коэффициентов С-С в указанную сторону. Однако такие фальсификации не являются необходимыми – то есть указанные отклонения могут происходить и по другим причинам. Более того, некоторые явные фальсификации отклоняют коэффициенты С-С в другую сторону!
В работе [4] показано, что если распределение голосов и явка являются не зависящими друг от друга случайными величинами, отклоняющимися от своих средних равновероятно в ту и другую сторону, то математические ожидания удовлетворяют условиям \(Ma_j = v_j; Mb_j = 0\). Наоборот, если имеется положительная зависимость доли голосов за победителя от явки (что, в частности достигается путем фальсификаций вида А-Г), то \(Ma_j\) отклоняется от \(v_j\) в большую сторону, а \(Mb_j\) от 0 в меньшую сторону. В работе [2] представлены результаты имитационных экспериментов, подтверждающие этот вывод. Значение линейного коэффициента С-С \(a_j\) равное \(v_j\) и значение коэффициента \(b_j\) равное нулю будем называть их сбалансированными значениями.
Таким образом, метод С-С может применяться для выявления подозрений на фальсификации, но не может служить утверждением о наличии фальсификаций. Кроме того, у метода С-С имеется ряд недостатков с точки зрения его применимости для выявления фальсификаций.
Во-первых, он очень чувствителен к статистическим «выбросам», то есть к результатам, сильно отклоняющимся от линии регрессии. Это особенно сказывается на российских выборах, поскольку в России такие выбросы обеспечиваются «закрытыми» участками – больницами, СИЗО и пр. Во-вторых, метод С-С не может служить показателем фальсификаций в случае сильных неоднородностей в электоральном поведении групп избирателей, в частности, при наличии реальных различий в электоральном поведении, обуславливающих связь явки с голосованием за определенного кандидата.
Примером плохой применимости метода С-С являются выборы в Берлине. Там до сих пор сохраняется разница в электоральном поведении западных и восточных берлинцев; восточные берлинцы менее охотно ходят на выборы, и менее охотно голосуют за ХДС. Поэтому значение линейного коэффициента С-С у ХДС в целом по Берлину значительно превышает долю голосов, набранных ХДС (например, на выборах в Бундестаг 2013 г. – это 50% и 27% соответственно).
Чувствительность метода С-С к набору участковых избирательных комиссий (УИК) хорошо иллюстрируется рисунком 1, на котором изображены данные УИК на выборах мэра Москвы в 2013 г.: по горизонтальной оси – явка, по вертикальной – доля голосов, полученных кандидатом Навальным, исчисленная от общего числа избирателей на избирательном участке. Наклон регрессионной прямой, проведенной через точки всех УИК, равен 9% (т.е. существенно меньше, чем набранная Навальным доля голосов). Если отбросить УИК с явкой более 75% (которых всего 5%), то наклон регрессионной прямой будет равен 27%, т.е. будет в точности равен набранной доле голосов. Если же отбросить УИК с явкой более 60% (которых всего 5,5%), то наклон регрессионной прямой будет равен 37%, что на 10% больше, чем набранная Навальным доля голосов.
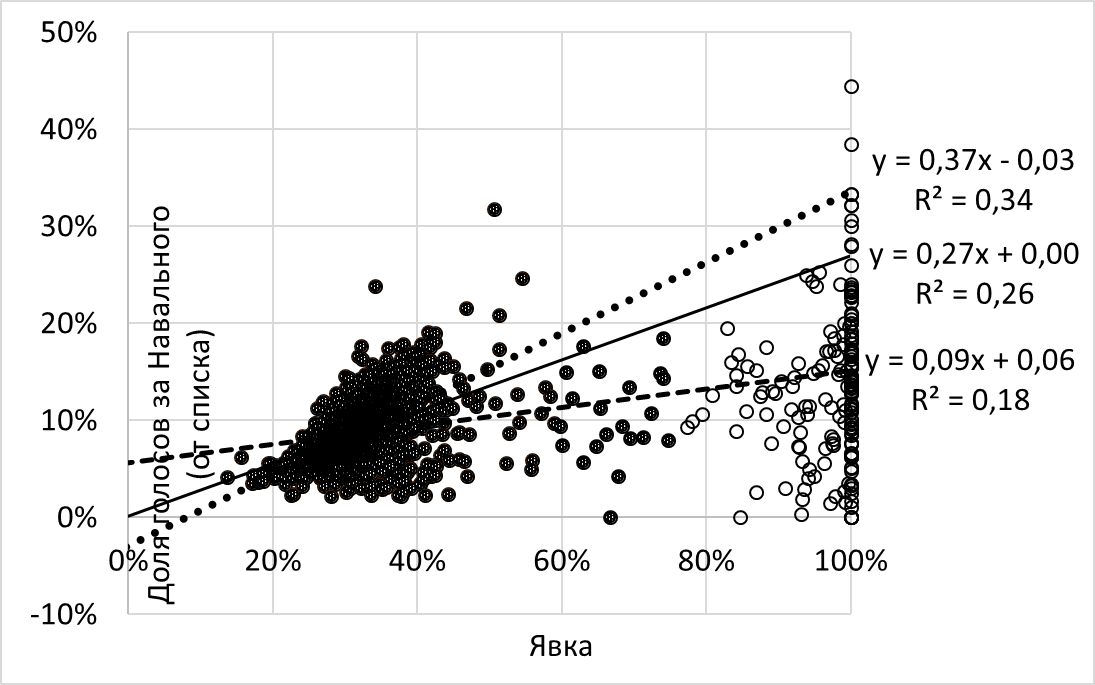
Рисунок 1. Результаты метода С-С при разных порогах отсечения участковых комиссий по явке
Модифицированный метод Собянина-Суховольского
Отсюда напрашивается вывод о том, что имеет смысл рассматривать не сам по себе коэффициент С-С, а зависимость коэффициента линейной регрессии \(a_j(\tau)\) от порога отсечения по явке \(\tau\) (т.е. значение линейного коэффициента С-С, вычисленное для УИК, у которых явка не больше величины \(\tau\)). На рисунке 2 изображена такая зависимость для двух основных кандидатов на выборах мэра Москвы в 2013 г.
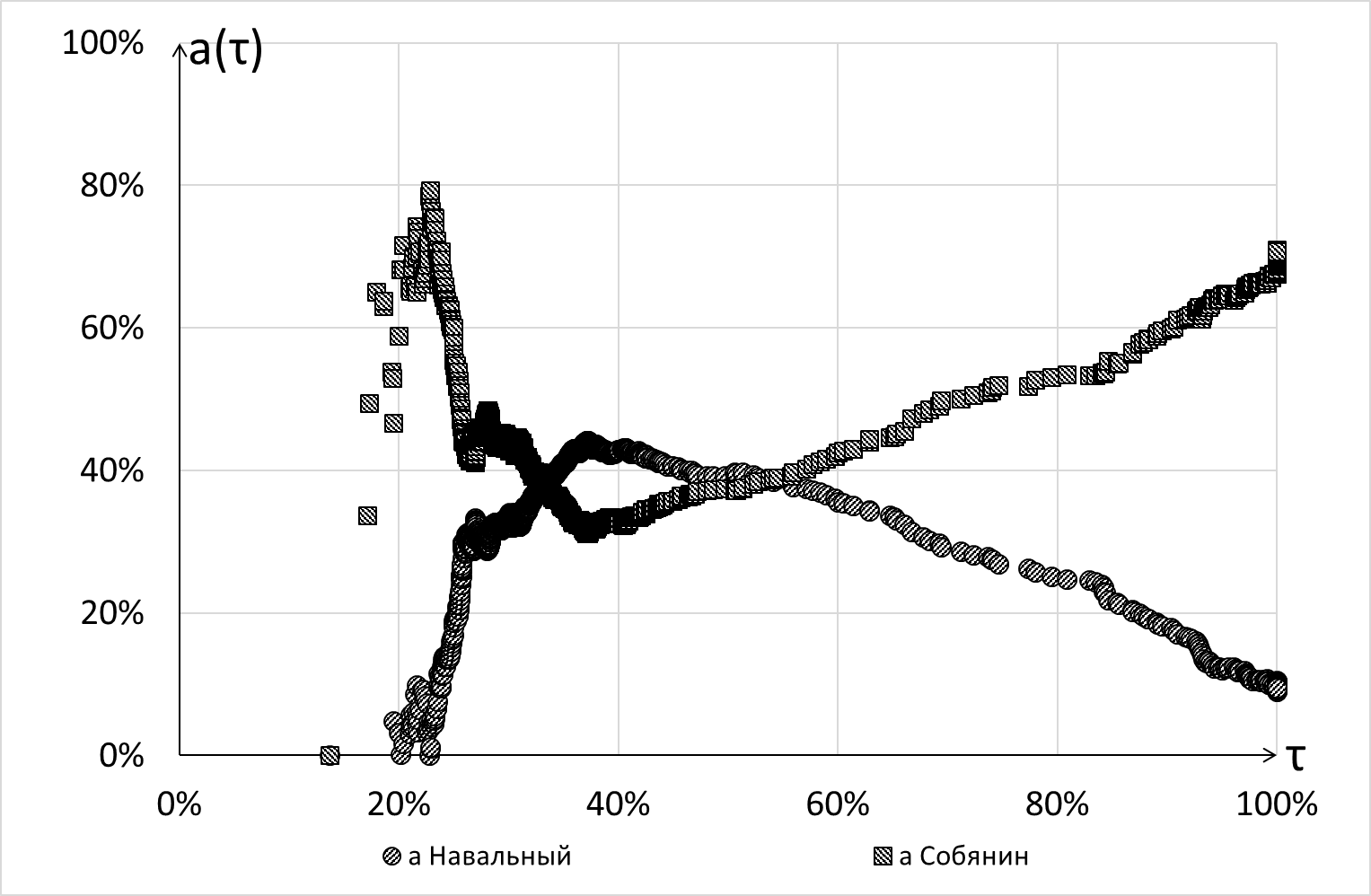
Рисунок 2. Зависимость коэффициента С-С от порога отсечения явки
Традиционный метод С-С заключается в том, что линейный коэффициент С-С сравнивают с долей голосов, набранных победителем, исчисленной от числа проголосовавших избирателей \(v_j\). Этот показатель также можно изобразить на графике в зависимости от порога отсечения явки. То же можно сделать и со свободным коэффициентом С-С \(b_j\). На рисунке 3 изображены три показателя в зависимости от порога отсечения явки \(\tau\) для кандидата Собянина С.С. (не путать с одним из авторов метода!) на выборах мэра Москвы в 2013 г., а на рисунке 4 – одновременно показатели и Собянина, и Навального.
Рисунок 4 позволяет сделать следующие выводы:
1) Традиционный метод С-С свидетельствует о наличии признаков фальсификаций (поскольку линейный коэффициент С-С при 100-процентной явке больше, чем доля голосов, набранная Собяниным, а свободный коэффициент С-С при 100-процентной явке меньше нуля), однако, если учитывать только участки с явкой до 55%, то этот метод говорит о признаках фальсификаций в пользу Навального.
Этот факт демонстрирует, что традиционный метод С-С следует использовать с большой осторожностью.
2) Примерно до явки 37% доля голосов за Навального возрастала, а затем стабилизировалась. Коэффициенты С-С демонстрируют этот эффект более отчетливо, чем показатель \(v\), поскольку они более чутко реагируют на порог явки.
3) Кривые показателей для Собянина и Навального симметричны. Это связано с тем, что остальные кандидаты не конкурировали с этими двумя. Голоса избирателей в основном распределялись между Собяниным и Навальным. Голосование за других кандидатов, а также наличие недействительных бюллетеней нарушит симметрию этих кривых.
4) При любом пороге явки кандидат Собянин по доле набранных голосов опережает кандидата Навального. Однако существует такая область спектра явки, в которой линейный коэффициент С-С Навального больше линейного коэффициента С-С Собянина, а свободный коэффициент С-С Навального меньше нуля. В этой области прирост явки давал больше преимущества Навальному, чем его сопернику.
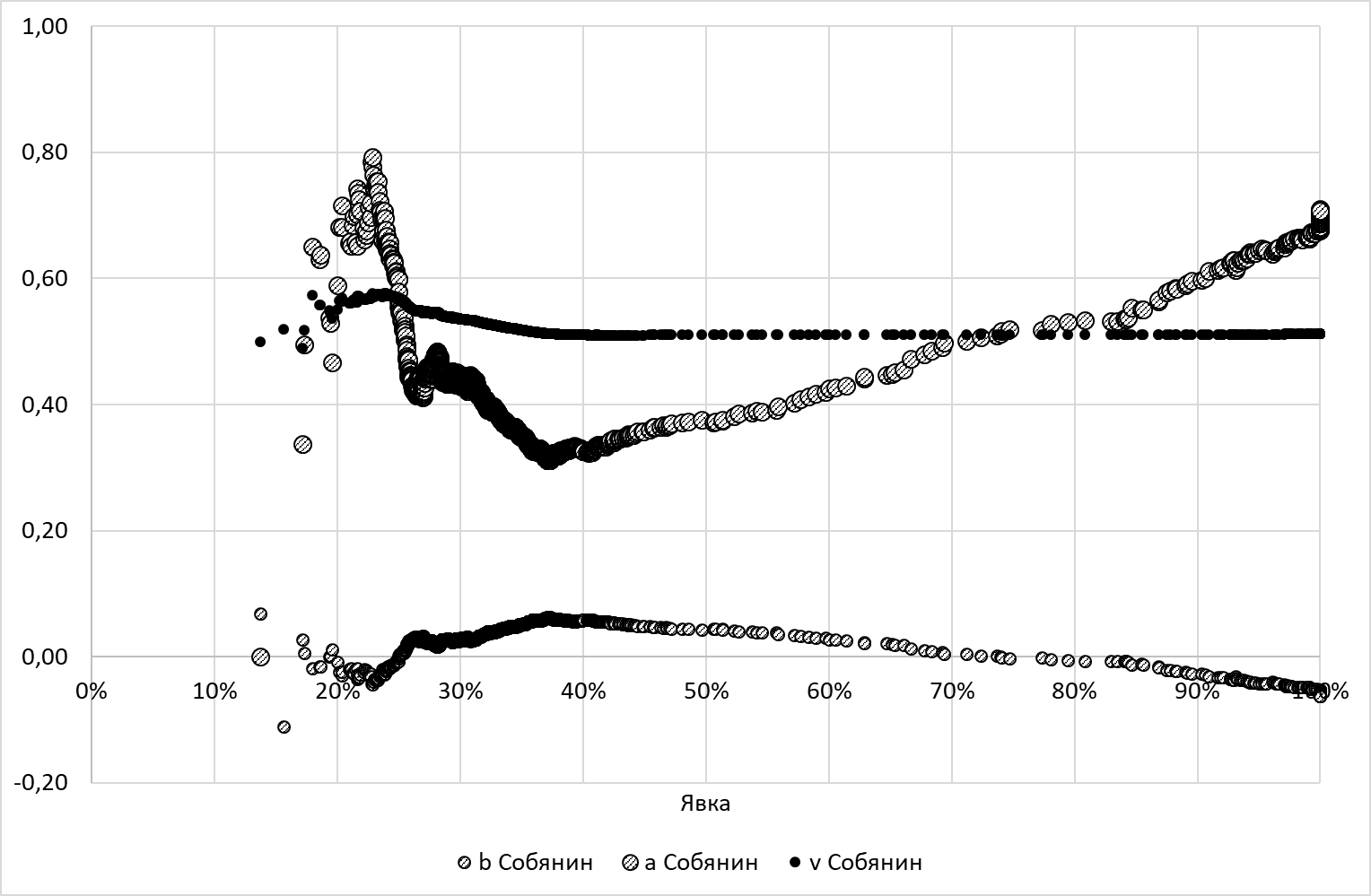
Рисунок 3. Зависимость электоральных показателей кандидата Собянина от явки
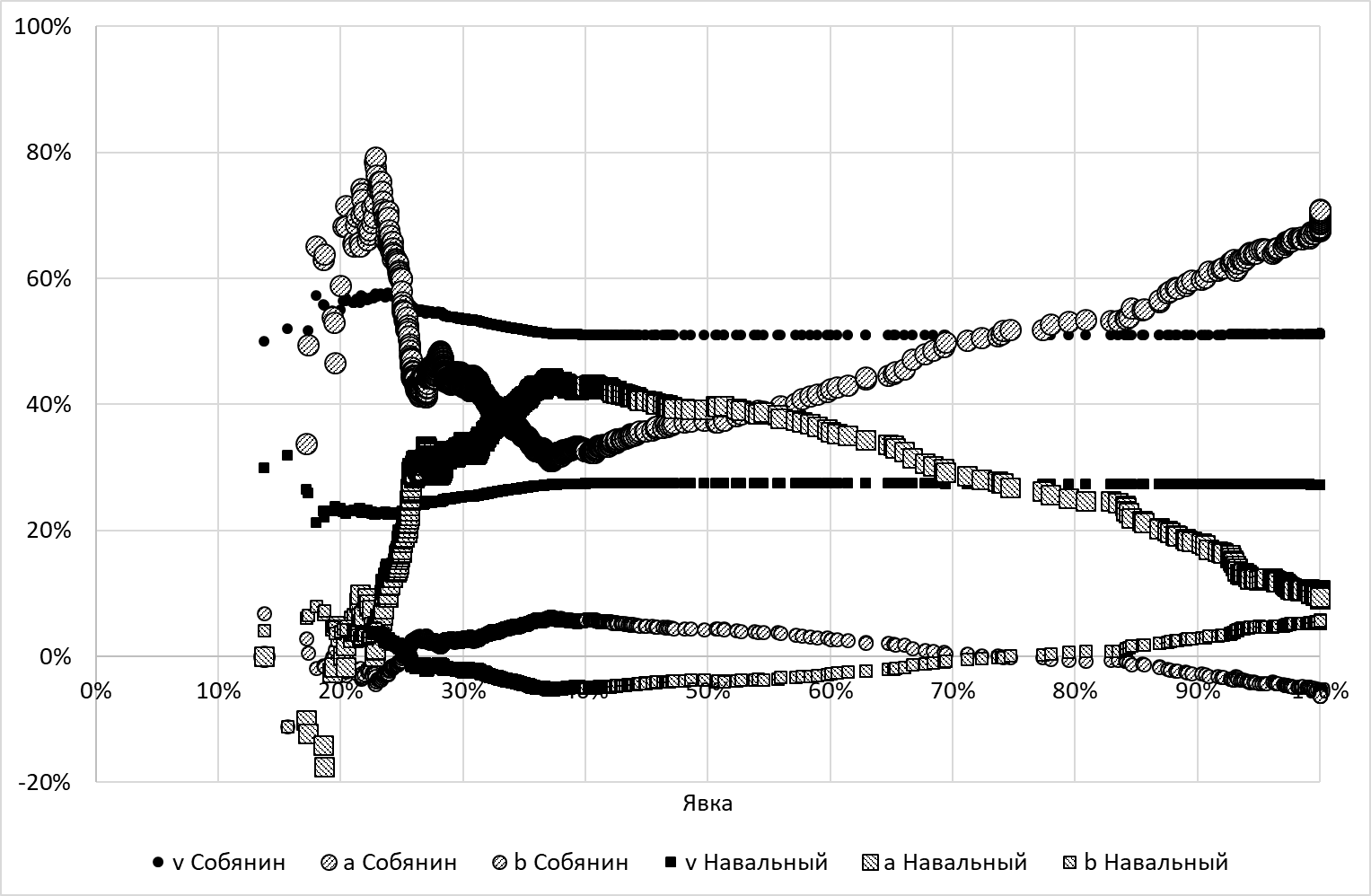
Рисунок 4. Зависимость электоральных показателей кандидатов Собянина и Навального от явки
Имитационные эксперименты
Чтобы проиллюстрировать поведение показателей \(v\), \(a\) и \(b\), была проведена серия имитационных экспериментов. Списочный состав избирательных комиссий (УИК) и их число (3374) были взяты непосредственно из данных официальной статистики по выборам мэра Москвы 2013 г.
Поведение избирателей имитировалось следующим образом: каждый избиратель принимал для себя решение об участии в выборах с вероятностью \(q_i\), зависящей от номера \(i\) избирательного участка, к которому приписан избиратель. Избиратель, который принял решение голосовать, выбирал из трех вариантов: с вероятностью \(p_0\) он голосовал недействительным бюллетенем (что имитировало также голосование за всех других кандидатов, кроме первого и второго), с вероятностью \(p_{i1}\) (зависящей от номера УИК, к которой приписан избиратель), он голосовал за первого претендента (мы используем это слово для кандидата или избирательного объединения), и с вероятностью \(1 - p_0 - p_{i1}\) избиратель голосовал за второго претендента. Вероятность \(p_0\) недействительного голосования мы полагали во всех экспериментах равной 5%.
Эксперименты различались зависимостью вероятностей \(q_i\) и \(p_{i1}\) от \(i\), имитировавшей электоральные различия между избирательными участками (территориями). В частности, эти зависимости могли описывать статистическую зависимость величин \(q_i\) и \(p_{i1}\).
Некоторые эксперименты имитировали фальсификации либо в форме вброса случайного числа бюллетеней в части комиссий, либо в форме «переброса» (то есть перемещения части голосов, поданных за второго претендента, к первому претенденту) случайного числа голосов в части комиссий.
Эксперимент №1. Квазиоднородные честные конкурентные выборы
В этом эксперименте имитировалось общество, в котором величина \(q_i\) является нормальной случайной величиной с заданными математическим ожиданием \(M\) и стандартным отклонением \(\Sigma\) (мы, естественно, заменяем \(q_i\) нулем или ста процентами, если эта случайная величина оказалась меньше нуля или больше 1 соответственно). Вероятность \(p_{i1}\) голосования за первого претендента – также нормальная случайная величина с заданными математическим ожиданием \(m\) и стандартным отклонением \(\sigma\). Таким образом, в этом эксперименте мы имитируем более-менее однородное (квазиоднородное) сообщество, в котором явка и голосование за кандидатов являются независимыми случайными величинами. (Еще более однородное сообщество получилось бы, если бы \(q_i\) и \(p_{i1}\) вообще не зависели от \(i\) - см. эксперимент 3; квазиоднородное сообщество представляется нам более реалистичным).
На рисунке 5 представлено поведение исследуемых показателей в одном из экспериментов с \(M\)=40%, \(\Sigma\)=20%, \(m\)=60%, и \(\sigma\)=40% (это означает, что средняя вероятность голосования за второго претендента равна 35%). Легко видеть, что в данном случае линейный коэффициент С-С \(а\) совпадает при высоком пороге отсечения явки с показателем \(v\), а свободный коэффициент \(b\) близок к нулю. При этом доля победителя совсем не равна 60%. Важно то, что линейные коэффициенты С-С у кандидатов значительно колеблются в областях средней явки и даже иногда пересекаются. Это говорит о высоком уровне конкуренции.
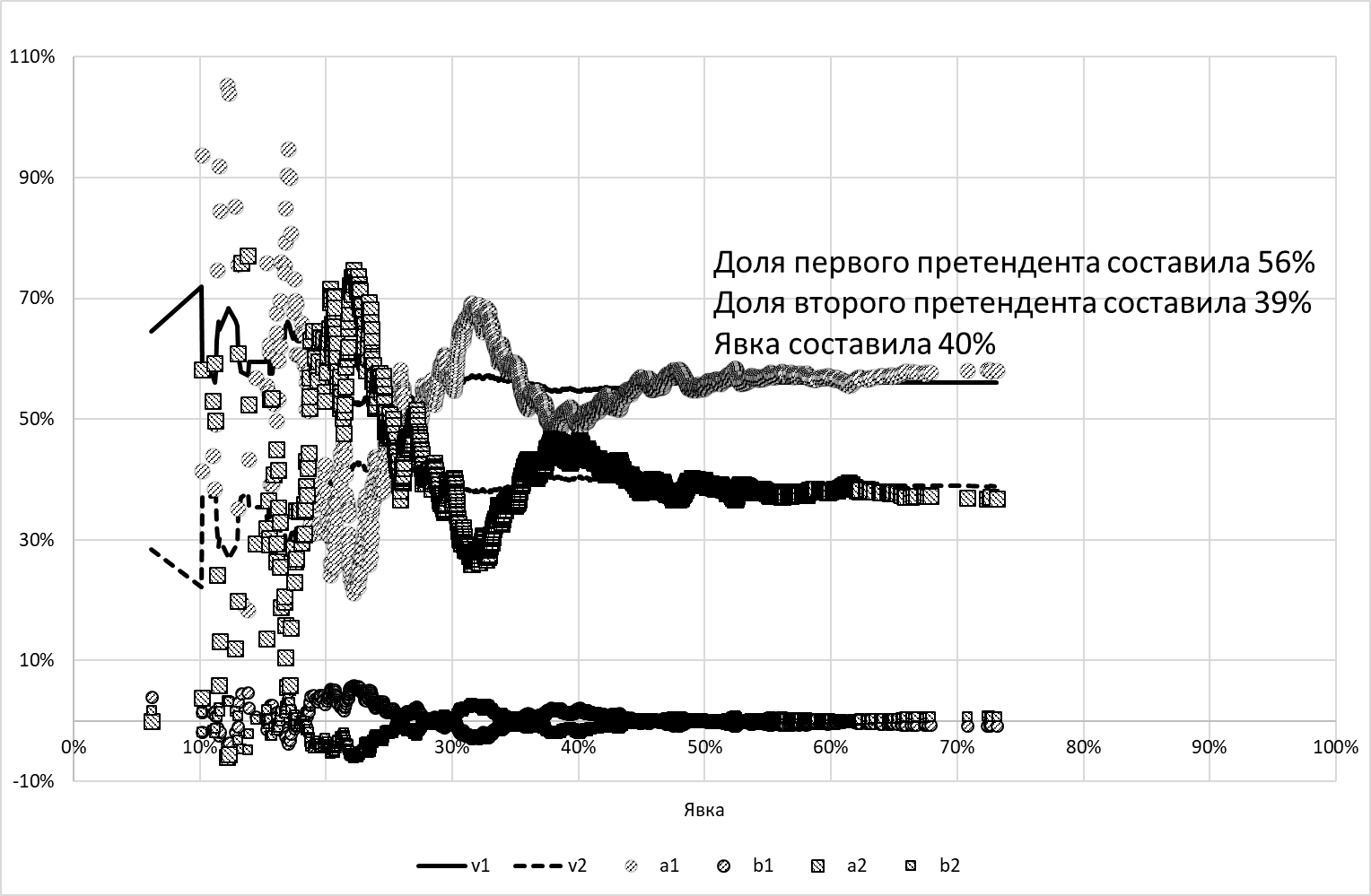
Рисунок 5. Результат эксперимента №1
Однако следует отметить, что повышение уровня однородности явки (т.е. уменьшение величины \(\Sigma\)) может приводить к отклонению коэффициентов С-С от сбалансированных значений.
Эксперимент №2. Неоднородные честные конкурентные выборы
Если существует статистическая связь между явкой и голосованием за кандидата (а такая связь может объясняться разными причинами), то коэффициенты С-С претерпевают отклонения от сбалансированных значений.
Разделим избирательные комиссии на две неравные группы: в первую входят 95% УИК, а во вторую – всего 5%. У первой группы величина \(q_i\) является нормально распределенной случайной величиной с \(M\)=40%, \(\Sigma\)=10%, а среднее голосование за первого претендента – нормальной случайной величиной с \(m\)=47,5% и \(\sigma\)=40% (т.е. в этой группе средняя доля голосования за первого и второго претендентов одинакова). У второй группы величина \(q_i\) является нормально распределенной случайной величиной с \(M\)=80%, \(\Sigma\)=10%, а среднее голосование за первого претендента – нормальной случайной величиной с \(m\)= 80% и \(\sigma\)=40%. Таким образом, явка и голосование за претендентов являются статистически зависимыми величинами.
Изменение показателей в одном из таких экспериментов показано на рисунке 6.
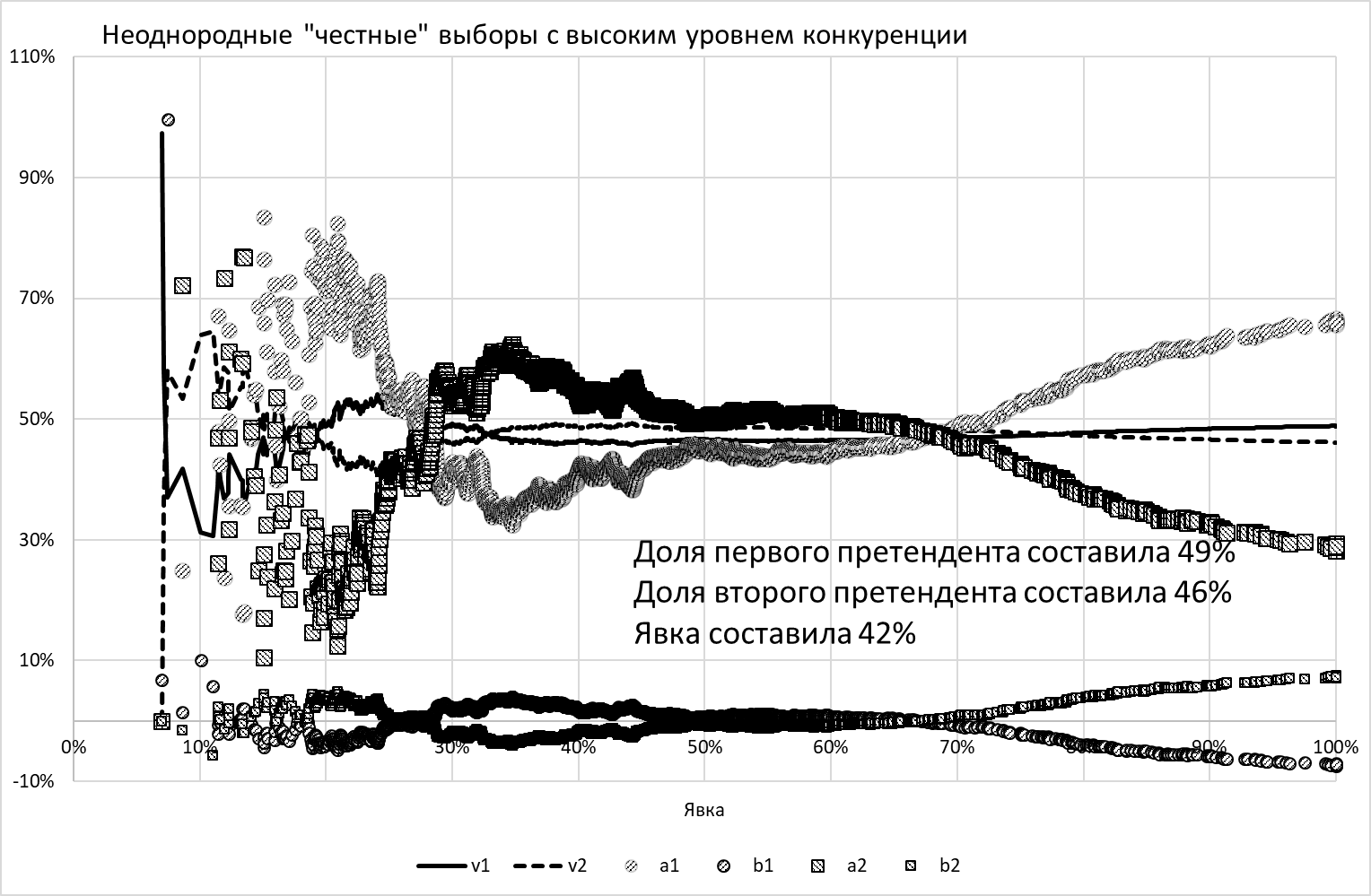
Рисунок 6. Результат эксперимента № 2
Видно, что всего 5% УИК со специфическими электоральными традициями сильно отклоняют коэффициенты С-С от сбалансированных значений.
Эксперимент №3. Однородные и квазиоднородные выборы со вбросом бюллетеней
Рисунок 7 представляет результат эксперимента со вбросом бюллетеней за первого претендента. Вброс заключается в том, что к реально выданным избирателям бюллетеням в половине УИК добавляется некоторое количество (в нашем случае – случайное число от 0 до 399) бюллетеней с отметкой за первого претендента.
В этом эксперименте мы умышленно сделали явку более однородной, т.е. положили \(\Sigma\)=0 при \(М\)=40%. Это позволило сделать эффекты отклонения \(а\) от \(v\), а \(b\) от нуля более яркими. Голосование за первого и второго претендентов было в среднем равновероятным (\(m\)=47,5%; \(\sigma\)=40%).
Однако если явка не будет такой однородной, как в предыдущем эксперименте, например, если положить \(\Sigma\)=40% при \(М\)=40%, то поведение коэффициентов С-С не покажет эффекта от вброса - см. рисунок 8.
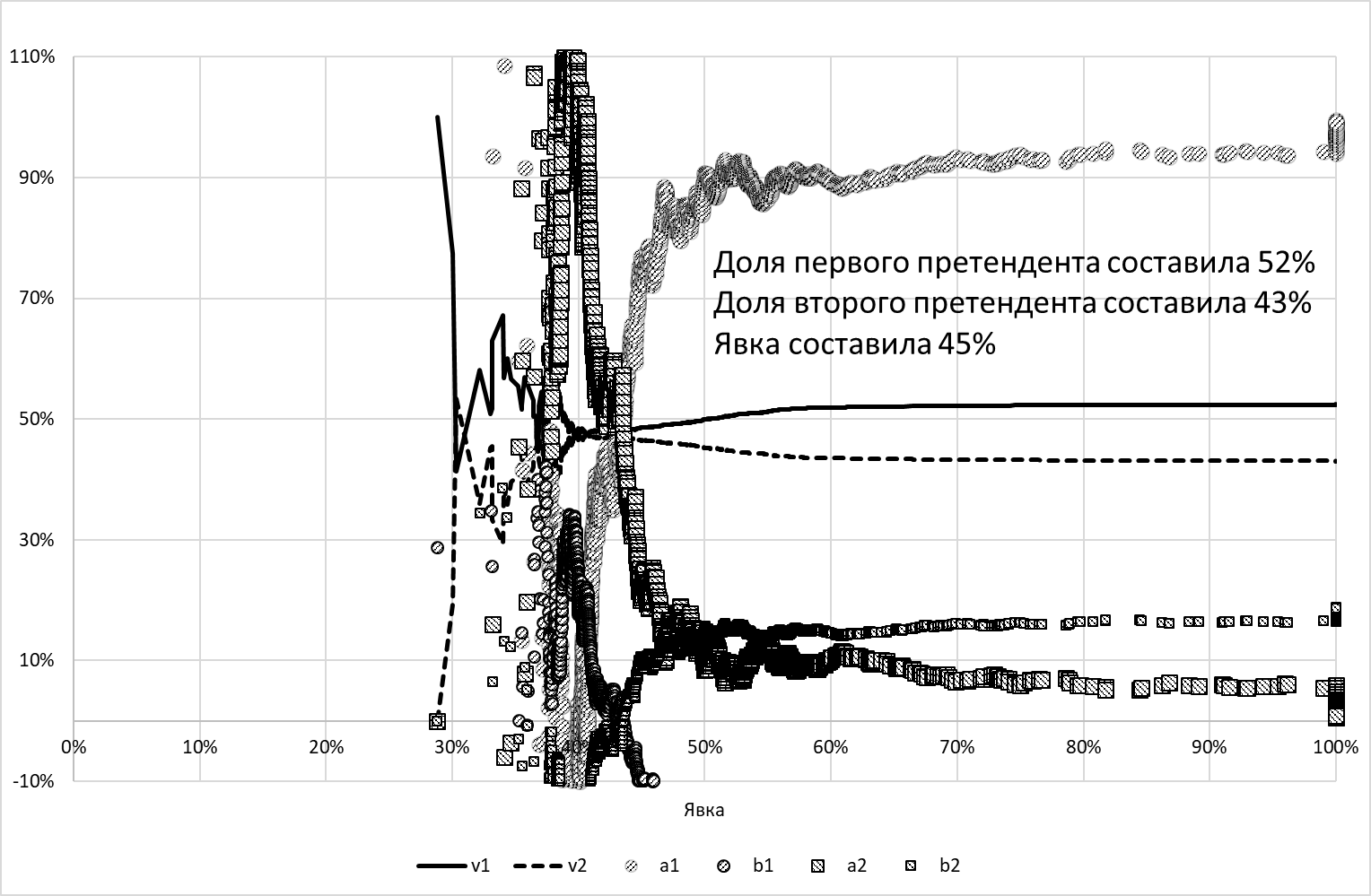
Рисунок 7. Результат эксперимента №3
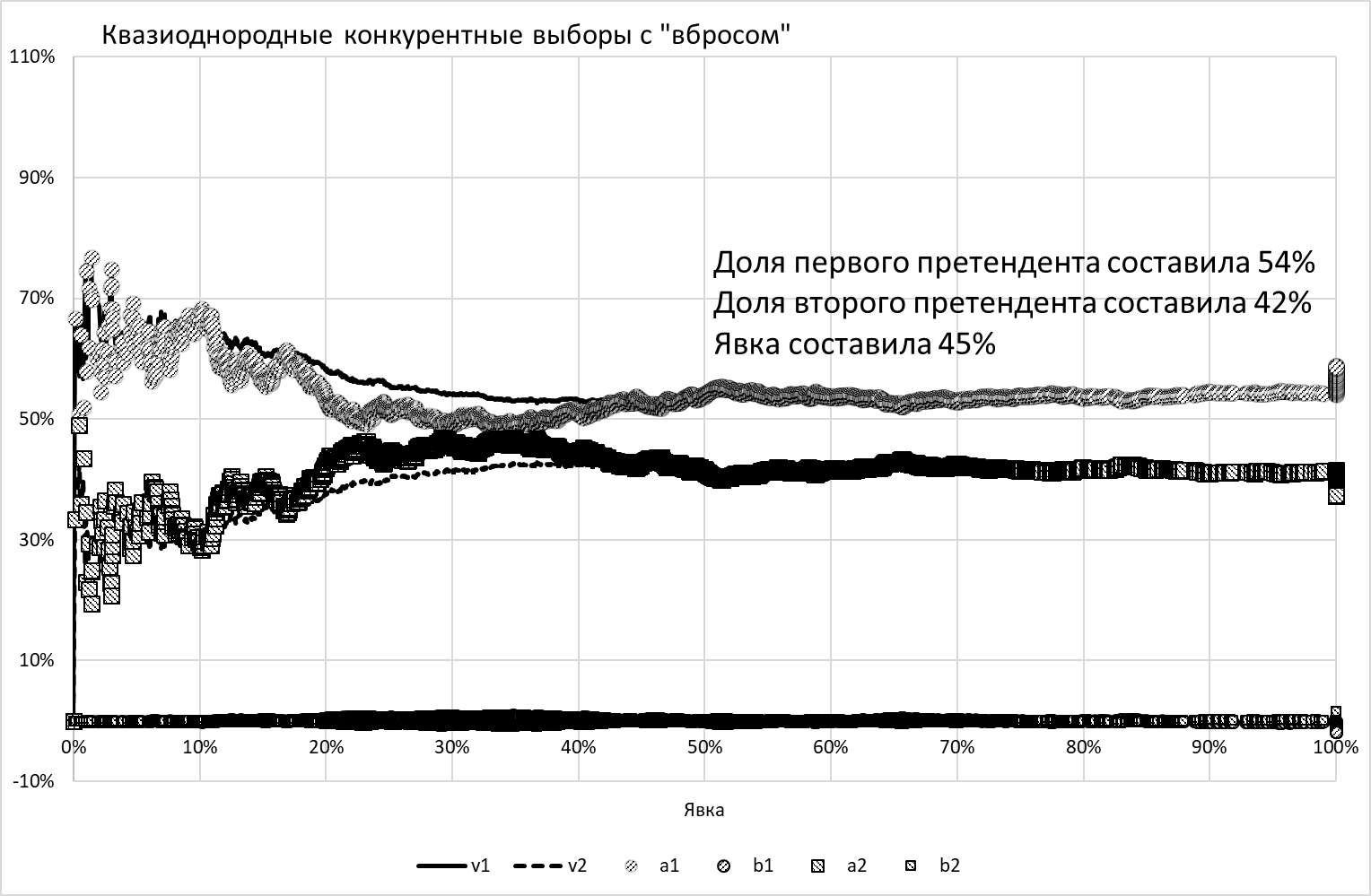
Рисунок 8. Результат эксперимента №3
Эксперимент №4. Однородные конкурентные выборы с «перебросом»
На рисунке 9 представлено поведение исследуемых показателей в эксперименте с \(M\)=40%, \(\Sigma\)=10%, \(m\)=47,5% и \(\sigma\)=40% (равновероятное в среднем голосование за обоих претендентов). В половине избирательных комиссий при подсчете голосов от второго претендента отнимается случайное число от 0 до 399 голосов, и они передаются первому претенденту (естественно, учитывается, что число голосов не должно быть меньше нуля).
Наблюдается интересный эффект: показатель \(а\) у победителя становится меньше показателя \(v\), а показатель \(b\) становится больше нуля. Таким образом, традиционный вывод метода С-С здесь неверен, точнее, признаком фальсификации является отклонение коэффициента \(а\) от \(v\) в меньшую сторону, а коэффициента \(b\) в положительную область. Это, между прочим, означает, что умелым сочетанием вброса и «переброса» можно добиться того, что коэффициенты С-С будут принимать сбалансированные значения.
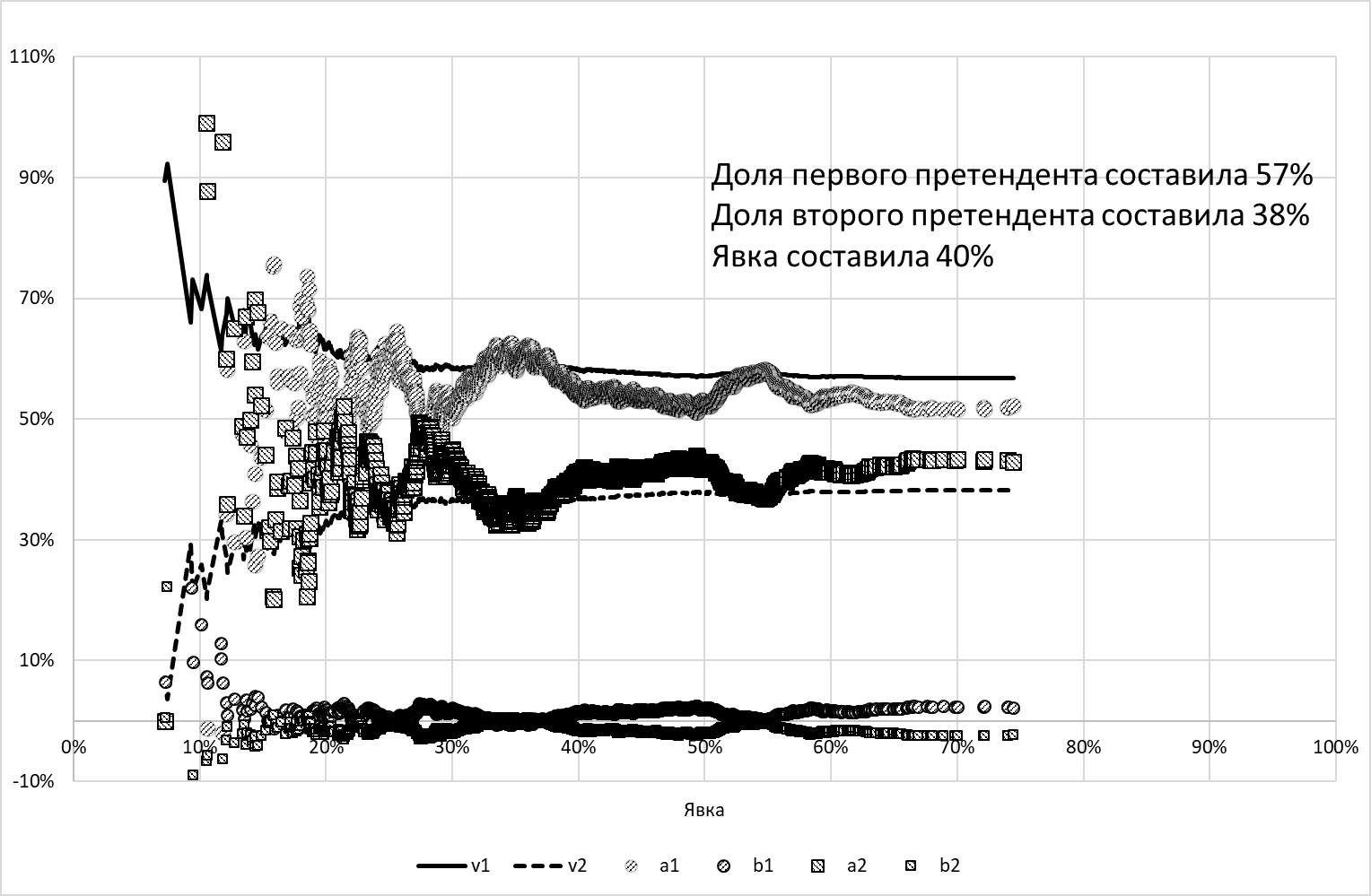
Рисунок 9. Результат эксперимента №4
Выводы
Традиционный метод Собянина-Суховольского плохо применим к поиску признаков фальсификаций по крайней мере, по трем причинам: во-первых, он очень чувствителен к статистическим «выбросам», во-вторых, он может порождать ложные признаки фальсификаций, и в-третьих, фальсификации типа переброса бюллетеней могут приводить к неправильным выводам. Однако в модифицированном виде, который обсуждается в этой статье, метод Собянина-Суховольского более полезен: характер поведения трех показателей – двух коэффициентов C-C и средней доли претендента \(v\) в зависимости от порога отсечения явки – может больше сказать о законности проведения голосования и подсчета голосов.
Имитационные эксперименты показывают, что характерное поведение коэффициентов С-С имеет вид, определяемый либо прямыми фальсификациями, либо территориальными неоднородностями в электоральном поведении. Поэтому по поведению этих коэффициентов, вычисленных на основе официальной электоральной статистики, можно делать предположения о наличии или отсутствии фальсификаций, или о наличии территориальных различий электорального поведения.
По поведению указанных коэффициентов можно также судить о том, в какой области значений явки имеются преимущества у того или иного претендента.
Отметим, что реальная российская электоральная статистика дает выразительные разнообразные примеры поведения указанных показателей.
Поступила в редакцию 26.04.2018, в окончательном виде 14.06.2018.
Список литературы
- Myagkov M., Ordeshook P.C., Shakin D. The Forensics of Election Fraud: Russia and Ukraine. New York: Cambridge University Press. 2009. 289 p.
- Бузин А.Ю. Влияние территориальных неоднородностей и фальсификаций на электоральные показатели. – Вестник РУДН, серия: математика, информатика, физика. 2014. №2. С. 72–80.
- Бузин А.Ю., Любарев А.Е. Преступление без наказания: Административные избирательные технологии федеральных выборов 2007–2008 гг. М.: ЦПК «Никколо М»; Центр «Панорама». 2008. 284 с.
- Кунов А., Мягков М., Ситников А., Шакин Д. Россия и Украина: нерегулярные результаты регулярных выборов, Аналитический доклад Института открытой экономики. М.: 2005. 37 с.
- Собянин А.А., Суховольский В.Г. Демократия, ограниченная фальсификациями: Выборы и референдумы в России в 1991-1993 гг.. М.: Проектная группа по правам человека. 1995. 268 с.
